![]() Molekülstruktur und Strukturparameter
Molekülstruktur und Strukturparameter
![]() Die asymmetrische Einheit
Die asymmetrische Einheit
![]() Allgemeine und spezielle Lagen
Allgemeine und spezielle Lagen
![]() Struktur und translatorische Symmetrie
Struktur und translatorische Symmetrie
In diesem Abschnitt wollen wir den Begriff Struktur klären. Das Wort Struktur wird oft mit sehr unscharfer Bedeutung gebraucht. Wir wollen den Begriff in scharfem, aber auch engerem Sinn verwenden, so wie es in der Molekülphysik, der Kristallphysik und insbesondere in der Kristallographie üblich ist: als die quantitative Beschreibung des Baus von Molekülen und Kristallen mit Hilfe geometrischer Parameter.
Die Lage eines Atoms bezüglich eines Koordinatensystems ist durch die
Angabe seiner drei Koordinaten definiert. Für ein N-atomiges
Molekül muss man also 3N Koordinaten angeben. Praktisch
verwendet man andere Koordinaten, nämlich
1. sechs äußere Koordinaten zur Festlegung von
Lage und Orientierung
des Moleküls;
2. 3N-6 interne Koordinaten zur
Beschreibung der inneren Beziehungen zwischen den Atomen.
Satz
1. Die Struktur von Molekülen wird durch geometrische Parameter, die so
genannten Strukturparameter, beschrieben. Als
Strukturparameter verwendet man Bindungslängen,
Bindungswinkel und
Diederwinkel.
2. Für ein nicht lineares, N-atomiges Molekül mit N ≥ 3
beträgt die Anzahl der Strukturparameter 3N-6.
3. Die Anzahl der unhängigen Strukturparameter wird durch Symmetrie
fast immer erniedrigt.
1. Für je zwei Atome können wir einen interatomaren Abstand
angeben. Wenn der interatomare Abstand einer chemischehn Bindung entspricht,
nennen wir ihn Bindungsabstand; er kann aber auch ein
nichtbindender Abstand sein.
2. Jeweils drei Atome spannen einen Winkel auf. Wenn
die drei Atome durch wenigstens zwei Bindungen verknüpft sind, sprechen
wir von Bindungswinkeln.
3. Jeweils vier Atome spannen einen Diederwinkel
oder Torsionswinkel auf.
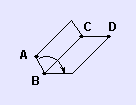
Der Betrag des Diederwinkels A-B-C-D (0 ≤ A-B-C-D ≤ 180°) ist der
Winkel zwischen den Ebenen A-B-C und B-C-D. Der Winkel wird positiv genommen,
wenn man sich beim Fortschreiten von A nach D im Uhrzeigersinn dreht,
andernfalls negativ.
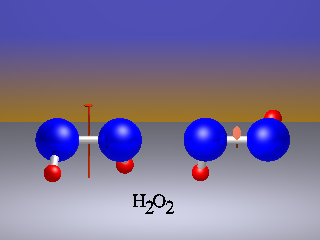
Wir betrachten als Beispiel das Wasserstoffperoxid-Molekül H2O2 (Abb.). Es besitzt eine zweizählige Symmetrieachse C2. Insgesamt brauchen wir für ein vieratomiges Molekül 6 Strukturparameter, nämlich hier im Beispiel die Bindungslängen O-O (1.49 Å) und O-H (0.97 Å, zweimal), den Bindungswinkel O-O-H (96°52', zweimal) und den Diederwinkel H-O-O-H (93°51'). Wegen der Symmetrie gibt es nur vier unabhängige Strukturparameter. Übrigens ist die Wahl der Strukturparameter zum Teil durch Intuition und Gepflogenheiten bestimmt. Man hätte als sechsten Parameter auch den nichtbindenden H..H-Abstand anstelle des Diederwinkels angeben können, nur wäre das weniger anschaulich.
Der Begriff der asymmetrischen Einheit stammt aus der Kristallographie. Wir wollen uns diesen Begriff zuerst an molekularen Beispielen klar machen und dann auf den Elementarbereich von Objekten mit translatorischer Symmetrie anwenden.
Definition
Als asymmetrische Einheit einer Struktur
bezeichnet man jede kleinste Teilstruktur, aus der die
Gesamtstruktur (des Objekts, des Moleküls, des Kristalls) durch
symmetrische Wiederholung erzeugt werden kann.
Wir betrachten zuerst zwei triviale Beispiele. Die asymmetrische Einheit des Methan-Moleküls ist die C-H-Baugruppe, die des CHBrClF-Moleküls das gesamte Molekül. Wenn die Symmetrie die Anzahl der unabhängigen Strukturparameter vermindert, dann ist auch die asymmetrische Einheit nur ein Teil der Gesamtstruktur.
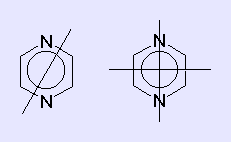
Wie die asymmetrische Einheit im Einzelfall zu wählen ist, wird durch die Symmetrie des Moleküls je nach Fall teilweise oder ganz festgelegt. Wir wollen dies am Beispiel des Pyrazins (ein C4H4N2) aufweisen. Dieses kleine heterocyclische Molekül ist hoch symmetrisch; intuitiv sehen wir, dass die asymmetrische Einheit eine CHN-Baugruppe umfassen wird. Die Abbildung zeigt, dass wir das Molekül zunächst halbieren können. Wenn wir diese Halbierung "richtig" vornehmen, können wir anschließend ein zweites Mal halbieren und erhalten als asymmetrische Einheit ein Viertel des Moleküls. Wenn wir dann noch ein symmetrieangepasstes Achsensystem in das Molekül hineinlegen, finden wir leicht und sicher, dass nur 5 Strukturparameter (statt 24 gemäß der allgemeinen Formel) die Gesamtstruktur vollständig definieren. Ein Molekülphysiker würde wahrscheinlich die Anzahl der zu bestimmenden cartesischen Koordinaten [x(C), z(C), x(H), z(H) und z(N)] abzählen, während der Chemiker eher nach einer Liste unabhängiger Bindungsparameter (Bindungslängen: C-C, C-N, C-H; Bindungswinkel: C-N-C, N-C-C) suchen würde.
Am Beispiel des BF3 ist sicher schon aufgefallen, dass die Anwesenheit einer dreizähligen Drehachse damit verbunden ist, dass wir drei Fluor-Atome haben. Dagegen liegt das Bor-Atom auf der Drehachse und ist nur einfach vorhanden. Diese Feststellung gibt den Anlass zu den folgenden Definitionen.
Definition
1. Ein Punkt der asymmetrischen Einheit, der sich auf einem oder mehreren
SEs befindet, besitzt eine spezielle Lage.
2. Ein Punkt der asymmetrischen Einheit, der sich auf keinem SE befindet,
besitzt eine allgemeine Lage.
3. Die Zähligkeit einer Lage ist die Anzahl
symmetrieäquivalenter Lagen.
4. Atome oder ebenso Gruppen, die sich in symmetrieäquivalenten Lagen
befinden, heißen chemisch äquivalent.
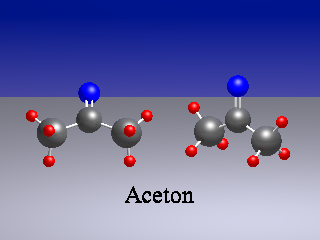
Wir machen uns die Bedeutung dieser Definitionen am Beispiel eines Aceton-Moleküls (CH3)2CO klar. Die Methyl-Gruppen des Moleküls können sich drehen. Die in der Abbildung gezeigte Rotationsstellung der Methyl-Gruppen entspricht dem Grundzustand des Moleküls.
Die Symmetrie ist hier die gleiche wie beim Wasser-Molekül.
1. Die Carbonyl-Gruppe liegt auf der C2-Achse und gleichzeitig
auf den beiden vertikalen Spiegelebenen. Diese Lage ist speziell und
einzählig; diese beiden Atome C und O gibt es nur einmal
im Molekül.
2. Je eine C-H-Bindung an den beiden äußeren Kohlenstoff-Atomen
liegt in einer der beiden Spiegelebenen. Auch diese Lage
ist speziell; sie ist zweizählig.
3. Schließlich gibt es noch vier H-Atome, die außerhalb der
Zeichenebene liegen. Diese Lage ist allgemein und vierzählig. Wir
können auch sagen: Die Lagen vorn-links, hinten-links, vorn-rechts und
hinten-rechts sind symmetrieäquivalent.
4. Die beiden Methyl-Gruppen sind chemisch äquivalent. Es ist ebenso
klar, dass es zwei Arten von C-Atomen gibt; diese unterscheiden sich z.B. in
ihrem Atomradius oder in der NMR-Spektroskopie in ihrer chemischen
Verschiebung.
Der Begriff der asymmetrischen Einheit wird in gleicher Weise auf Systeme mit translatorischer Symmetrie angewendet. Wir betrachten als einfaches Beispiel ein Bandornament.

Die Abbildung haben zeigt ein spiegelsymmetrisches Muster. Wenn der Elementarbereich des Bandornaments Punktsymmetrie besitzt, genügt bereits ein Teil des Elementarbereichs (je nach Symmetrie eine Hälfte oder ein Viertel) zur Erzeugung der Gesamtstruktur. In der zweiten Abbildung ist ein geeigneter Elementarbereich (links) ist so gewählt, dass die Punktsymmetrie (Drehsymmetrie und Lateralsymmetrie) des Mäanders voll berücksichtigt wird. Die Lateralsymmetrie erlaubt eine Halbierung des Elementarbereichs (mittig). Die Drehsymmetrie erlaubt eine zweite Halbierung und ergibt die asymmetrische Einheit des Ornaments (rechts). Die asymmetrische Einheit umfasst hier also ein Viertel des Elementarbereichs.

Fazit:
Wenn translatorische Symmetrie vorliegt, wird das Strukturproblem in zwei
Stufen reduziert. In der ersten Stufe gehen wir von der unendlich
ausgedehnten Idealstruktur zu einem (endlichen) Elementarbereich. Wenn
weitere Symmetrie vorliegt, gehen wir in einer zweiten Stufe zur
asymmetrischen Einheit.
Wir deuten hier nur noch an: Für eine Strukturbestimmung werden wir Zellparameter brauchen, welche die Geometrie des Elementarbereichs beschreiben, und ferner Lagekoordinaten, welche den Inhalt der asymmetrischen Einheit charaterisieren. Im Fall unseres Bandornaments sind die Lagekoordnaten die Koordinaten der Pixel; bei einer kristallinen Substanz sind es die Koordinaten der Atome in der asymmetrischen Einheit.