Zum Inhaltsverzeichnis
2.6.1. Drehachsen
2.6.2. Inversionsachsen
2.6.3. Schlussbemerkungen und Resumé
Im Kapitel 2.1 haben wir das Nebeneinander von Schoenflies-System und Hermann-Mauguin-System erläutert. Wir können
uns jetzt dem Hermann-Mauguin-System zuwenden. Wir tun dies
– ausgehend vom sicheren Grund des Schoenflies-Systems und
– nur so weit, wie es die Beschreibung der Punktsymmetrien erfordert.
Im vorliegenden Kapitel betrachten wir die Symmetrieelemente. Im nächsten Kapitel folgen dann die Punktgruppen.
Die Drehachsen werden genau wie im Schoenflies-System definiert. Der einzige Unterschied besteht in der Art der Symbole: Eine n-zählige Drehachse wird durch die ganze Zahl n dargestellt. Es besteht also die folgende (ganz triviale) Entsprechung der Symbole:
| 1 | 2 | 3 | 4 | 5 | 6 |
| C1 | C2 | C3 | C4 | C5 | C6 |
In diesem Abschnitt betrachten wir Drehinversionen. Das sind Operationen, die aus einer Drehung und einer Inversion zusammengesetzt sind. Wir sagen auch: Drehinversionen entstehen durch Kopplung von Drehung und Inversion.
Bei den Drehinversionen der Zähligkeit n
führen wir eine Drehung um einen Drehwinkel von 2π/n
durch und gekoppelt damit eine Inversion. Das Symmetrieelement ist die Inversionsachse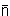 
mit der Zähligkeit n.
So wie es zu jeder Drehachse eine Drehspiegelachse gleicher Zähligkeit gibt, haben wir hier zu jeder Drehachse eine Inversionsachse gleicher Zähligkeit. Zu jeder Inversionsachse muss es also eine Drehspiegelachse gleicher Wirkung geben. Wir erwarten auch, dass es drei Klassen von Inversionsachsen geben wird, so wir wir drei Klassen von Drehspiegelachsen haben. Es besteht die folgende Korrespondenz:
 |
 |
 |
 |
 |
 |
 |
 |
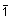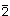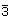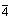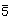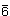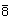| S2 | S1 | S6 | S4 | S10 | S3 | S8 | S5 |
Man kann diese Korrespondenz verifizieren, indem man Stereogramme mit Hilfe der oben gegebenen Definition der Drehinversionen konstruiert und mit den früher für die Drehspiegelachsen erhaltenen Stereogrammen vergleicht. Wir empfehlen, dies für die Zähligkeiten n = 3, 4 und 6 tatsächlich zu tun.
Die drei Klassen von Inversionsachsen
1. Inversionsachsen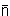
mit ungeradem n (n = u) oder n = 1, 3, 5, ...
Diese Inversionsachsen entsprechen den Drehspiegelachsen S2n
doppelter Zähligkeit.
2. Inversionsachsen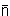
mit doppelt ungeradem n (n = 2u) oder n = 2, 6, ...
Diese Inversionsachsen entsprechen den Drehspiegelachsen Sn/2
halber Zähligkeit.
3. Inversionsachsen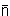
mit doppelt geradem n (n = 2g) oder n = 4, 8, ...
Diese Inversionsachsen entsprechen den Drehspiegelachsen Sn
gleicher Zähligkeit.
Zwei Sonderfälle:
– Die Inversionsachse 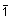entspricht einem Drehwinkel von 360°
bzw. von 0° und einer Inversion, also kurz einer Inversion; die Achsenrichtung ist nicht definiert.
– Die Inversionsachse 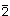entspricht einer Drehung um 180° gekoppelt mit einer
Inversion. Das ist, wie man leicht aus dem Stereogramm
ersehen kann, die Spiegelung an einer Ebene.
Für dieses Symmetrieelement verwendet man das Symbol m
(von englisch "mirror").
Die Idee der Inversionsachsen und die neuen Symbole sind gewöhnungsbedürftig. Solange man sich nur mit Punktsymmetrien befasst, scheint das Hermann-Mauguin-System gleichwertig, nur eben etwas anders. Erst bei den Kristallsymmetrien zeigt sich, dass Inversionsachsen günstiger als Drehspiegelachsen sind, weil sie eine logisch einfachere Beschreibung der Kristallsymmetrien erlauben.
Die Schoenflies-Bezeichnungen σh, σv und σd tragen bereits im Symbol Information über die räumliche Ausrichtung des Symmetrieelements relativ zu anderen Symmetrieelementen der gegebenen Punktgruppe. Im Hermann-Mauguin-System werden Spiegelebenen nicht durch ihren Namen, sondern durch ihre Anordnung im Punktgruppensymbol unterschieden. Wie das zu verstehen ist, werden wir im folgenden Kapitel sehen.
