Zum Inhaltsverzeichnis
2.2.1. Drehungen und Drehachsen
2.2.2. Drehspiegelungen und Drehspiegelachsen
2.2.3. Schlussbemerkungen und Resumé
In diesem Kapitel wollen wir die Symmetrieoperationen und Symmetrieelemente der Punktsymmetrien systematisch aufzählen. Das ist für die Drehungen einfach. Für die komplizierteren Drehspiegelungen braucht man etwas Durchhaltevermögen.
Wir hatten uns im Abschnitt "Was ist Symmetrie?" die Wirkung einer dreizähligen Drehachse mit den zugehörigen Drehungen um 0, 120 und 240° vor Augen geführt. Es gilt nun, dieses Beispiel zu verallgemeinern.
Wir betrachten also allgemein Drehungen
Cn um einen Drehwinkel
von 2π/n. Dazu gehört als
Symmetrieelement die Drehachse Cn mit
der Zähligkeit n.
Es gibt demgemäß Drehungen:
Cn, Cn2, ...,
Cnn = E
für Drehachsen Cn mit
n = 1, 2, 3, ...
Ein Punkt in allgemeiner Lage wird n
Mal wiederholt.
Durch Konvention legen wir fest: Eine einzelne Drehachse wird stets senkrecht gestellt.
Die Symmetrieeigenschaften von Symmetrieelementen (und ebenso von Punktgruppen) werden sehr kompakt durch Stereogramme dargestellt, hier konkret für die Drehachsen C2, C3 und C4.
Mehr zu den Stereogrammen von Drehachsen
Zwei Sonderfälle:
– Die Drehung C1 entspricht
einem Drehwinkel von 360°
bzw. von 0°. Es gilt also C1 = E. Die Richtung
einer Drehachse C1 ist nicht definiert. Ein unsymmetrisches
Objekt hat keinerlei sonstige Symmetrie. Dieser Fall der Unsymmetrie ist einerseits trivial, andererseits sind es
oft gerade die trivialen Fälle, die man als wenig anschaulich oder als
nicht leicht einsehbar oder als der Vernunft widersprechend empfindet.
– Die Drehung C∞
entspricht einem unendlich kleinen
Drehwinkel und beliebigen Vielfachen davon. Alle rotationssymetrischen
Objekte wie Zylinder und Kegel sowie alle linearen Moleküle haben eine
solche Drehachse; die Kugel besitzt sogar unendlich viele davon.
In den Übungen findet man Beispiele von Alltagsobjekten und von Molekülen. Manchmal ist die Symmetrie mit einer einzigen Drehachse vollständig beschrieben (Beispiel: H2O2), manchmal gibt es noch andere, zusätzliche Symmetrie (Beispiel: H2O).
In diesem Abschnitt betrachten wir Drehspiegelungen. Das sind Operationen, die aus einer Drehung und einer Spiegelung an einer Ebene senkrecht zur Drehachse zusammengesetzt sind. Wenn man eine neue Symmetrieoperation dadurch definiert, dass zwei Operationen zusammen durchgeführt werden müssen, spricht man von Kopplung (auch Koppelung) von Operationen.
Bei den Drehspiegelungen
Sn führen wir eine Drehung Cn
um einen Drehwinkel von 2π/n
und gekoppelt damit eine Spiegelung σh an einer Ebene senkrecht zur Drehachse
(meist der Äquatorebene) durch:
Sn = (Cnσh) =
(σhCn). Das
Symmetrieelement ist die Drehspiegelachse Sn mit
der Zähligkeit n.
Auch hier gilt durch Kovention: Eine einzelne Drehspiegelachse wird senkrecht vorgestellt. Die Spiegelebene steht dann waagerecht oder horizontal; daran erinnert das Subskript "h".
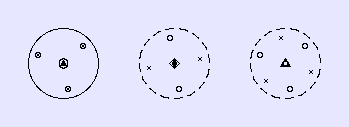
Wir schauen nun die Drehspiegelsymmetrien für n = 3, 4 und 6 mit Hilfe ihrer Stereogramme an, also für die Drehspiegelachsen S3, S4 und S6.
Mehr zu den Stereogrammen von Drehspiegelachsen
Der erste Blick auf die Stereogramme zeigt: Die drei Beispiele haben wenig gemeinsam. Wenn eine Symmetrieoperation mit Hilfe gekoppelter Operationen definiert ist, kann es so sein, dass die beiden Operationen selbst schon Symmetrieoperationen sind. Diese Situation finden wir bei der Drehspiegelung S3: Sowohl die Drehung C3 wie auch die Spiegelung σh sind für sich genommen Symmetrieoperationen. Es kann aber auch so sein, dass die beiden Operationen für sich genommen keine Symmetrieoperationen sind. Diese zweite Situation finden wir bei den Drehspiegelungen S4 und S6: Man findet Drehachsen mit nur halber Zähligkeit und die Ebene senkrecht zur Drehachse, an der gespiegelt wird, ist nicht ein Symmetrieelement.
Jedes der drei Beispiele steht für eine ganze Klasse von Drehspiegelungen bzw. von Drehspiegelachsen. Wir raten dazu, diese Verallgemeinerung hier nur Kenntnis zu nehmen. Im Kapitel "Punktgruppen: Die Systematik nach Schoenflies" wird man einen Verweis auf eine genauere Analyse finden.
Die drei Klassen von Drehspiegelungen bzw. Drehspiegelachsen
1. Drehspiegelungen mit ungeradem n (n = u) oder n = 1, 3, 5, ...
Man erkennt eine Drehachse Cn und eine horizontale Spiegelebene
σh. Ein Punkt in allgemeiner Lage wird 2n
Mal wiederholt. Oder: Die allgemeine Punktlage ist 2n-zählig.
2. Drehspiegelungen mit doppelt ungeradem n (n = 2u) oder n = 2, 6, 10, ...
Man sieht eine Drehachse halber Zähligkeit Cn/2 und ein
Symmetriezentrum i. Die allgemeine Punktlage ist n-zählig.
3. Drehspiegelungen mit doppelt geradem n (n = 2g) oder n = 4, 8, 12, ...
Man findet auch hier eine Drehachse halber Zähligkeit Cn/2 und
eine n-zählige allgemeine Punktlage.
Drei Sonderfälle:
– Die Drehspiegelung S1 entspricht
einem Drehwinkel von 360° bzw. von 0° und einer Spiegelung an einer
Ebene. Das ist kurz die Spiegelung an einer Ebene:
S1 = σ.
– Die Drehspiegelung S2 entspricht
einer Drehung um 180° und der Spiegelung an einer Spiegelebene
σh. Das ist, wie man leicht aus dem Stereogramm
ersehen kann, die Inversion i: S2
= i. Die Richtung der Drehspiegelachse und ebenso die Orientierung der
Spiegelebene bleiben undefiniert.
– Die Drehspiegelung S∞
entspricht einem unendlich kleinen Drehwinkel
und beliebigen Vielfachen davon. Das ist wie bei der Drehung
Cn mit n unendlich. Beide sind notwendig mit zusätzlicher
Symmetrie verbunden. Bei der Drehachse kommen vertikale Spiegelebenen
σv dazu und zwar unendlich viele. Bei der Drehspiegelachse
kommt u.a. noch eine horizontale Spiegelebene σh dazu.
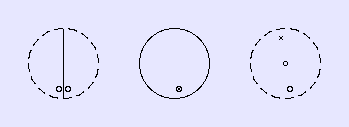
Die folgenden Stereogramme zeigen
– links eine vertikale Spiegelebene σv als
Schnittlinie mit der Äquatorebene;
– in der Mitte eine horizontale Spiegelebene σh, welche mit
der Äquatorebene zuammenfällt;
– rechts ein Symmetriezentrum, dargestellt durch einen kleinen Kreis in der
Mitte des Stereogramms.
Es gibt, wie wir in diesem Kapitel gesehen haben, zwei Arten von Symmetrieoperationen: die Drehungen und die Drehspiegelungen. Zwischen den beiden besteht ein grundsätzlicher Unterschied: Drehungen sind im physikalischen Raum durchführbar, Drehspiegelungen sind nur gedanklich durchführbar. Gedanklich heißt, dass die Symmetrieoperation an geometrischen oder überhaupt an mathematischen Objekten sowie an physikalischen oder chemischen Modellen und Formeln durchgeführt wird. Im Englischen spricht man von eigentlichen Drehungen (proper rotations) und uneigentlichen Drehungen für Drehspiegelungen (improper rotations) und betont damit den erwähnten grundsätzlichen Unterschied.
Die Symbole in den Stereogrammen der Symmetrieelemente sind in der folgenden Übersicht nochmals aufgezählt.
In vielen Texten werden die Spiegelung an einer Ebene und die Inversion eigenständig behandelt, wie auch wir es in dem einführenden Kapitel "1.2. Was ist Symmetrie?" getan haben. Das liegt nahe, weil diese beiden Operationen leichter zu verstehen sind als die Drehspiegelungen Sn mit n > 2. Hier, in diesem Kapitel, haben wir es jedoch vorgezogen, beide als spezielle Drehspiegelungen zu behandeln. Die Begriffe Spiegelung und Drehspiegelung werden dabei synonym und viele spätere Überlegungen werden dadurch logisch einfacher und straffer.
