Zum Inhaltsverzeichnis     Zurück zum Haupttext

Hinweis: Diese Übungen setzen voraus, dass die Nebenkapitel von Kapitel 1.4. bearbeitet worden sind.

Übung 1
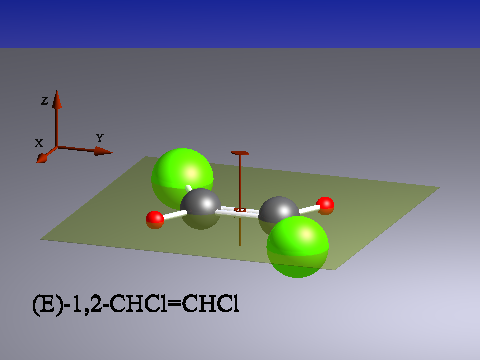
Wir betrachten hier nochmals das (E)-1,2-Dichlorethan-Molekül. Hier sind vier SOs möglich: E, C₂, σ_h und i. Diese Gruppe hat das Schoenflies-Symbol C_2h und im Hermann-Mauguin-System das Gruppensymbol 2/m, gesprochen "zwei über m". Die "2" steht für die zweizählige Drehachse und das "m" für die Spiegelebene m (engl. mirror). Der Schrägstrich zeigt an, dass der Spiegel senkrecht zur Drehachse steht.
Schreiben Sie alle eigentlichen Untergruppen der Gruppe C_2h an.

Übung 2
1. Wieviele Zeilen und Spalten muss die Gruppentafel der Gruppe C_2h haben? Was schreiben Sie links vor die Zeilen und oben über die Spalten?
2. Füllen Sie zuerst alle Produkte ein, die das Einheitselement als Faktor haben, dann alle Potenzen der Elemente und erst dann die verbliebenen gemischten Produkte.
3. Ist diese Gruppe Abelsch?
4. Vergleichen Sie die Gruppen C_2v und C_2h anhand ihrer Gruppentafeln. Was finden Sie heraus?

Übung 3
1. Das Molekül BF₃ besitzt eine dreizählige Drehachse C₃ und drei zweizählige Drehachsen C₂, C₂' und C₂". Die gleichen Drehungen sind an einem trigonalen Prisma möglich. Die Ecken des Prismas sind in allgemeiner Lage; deshalb ist das Prisma als Beispiel günstiger als BF₃. Welche Ordnung hat diese Gruppe?
2. Versuchen Sie, die Gruppentafel aufzustellen. Hinweis: Sie benötigen eine gute Zeichnung oder ein Modell des trigonalen Prismas. Die Ecken bezeichnen Sie mit Nummern oder Buchstaben. Die Lage der zweizähligen Achsen muss bezüglich der Ecken klar bezeichnet sein. Bei den Produkten ermitteln Sie die gemischten Produkte (z.B. C₃C₂ = C₂' und C₂C₃ = C₂") zuletzt; wenn einige Produkte bekannt sind, folgen die übrigen ohne Rechnung aus den allgemeinen Eigenschaften von Gruppentafeln.
3. Welchen wichtigen Unterschied zeigt Ihnen ein Vergleich mit den Gruppen C_2v und C_2h?

  Hilfe zu den Übungen und Ergänzungen

  smx-projekt@ac.rwth-aachen.de