![]() Definition
Definition
![]() Drehsymmetrie
Drehsymmetrie
![]() Spiegelsymmetrie
Spiegelsymmetrie
![]() Chiralität
Chiralität
![]() Translatorische Symmetrie
Translatorische Symmetrie
![]() Punktsymmetrie und Raumsymmetrie
Punktsymmetrie und Raumsymmetrie
In diesem Abschnitt definieren wir den Begriff Symmetrie und entwickeln erste grundlegende Vorstellungen.
Wir beginnen mit einem geometrischen Objekt (z.B. mit einer geometrischen
Figur oder einem geometrischen Körper) und erzeugen eine Abbildung. Für diese Abbildung verlangen wir zwei
Eigenschaften:
1. Entsprechende Abstände und Winkel im Objekt und in seinem Abbild
sollen gleich sein. Abbildungen, die dieser Bedingung genügen,
heißen Isometrien.
2. Die Lage von Objekt und Abbild sollen ununterscheidbar sein. Isometrien,
die zusätzlich dieser zweiten Bedingung genügen, heißen
Symmetrien.
Definition
Eine Deckoperation oder Symmetrieoperation (SO)
ist eine Abbildung, bei der das Objekt und sein Abbild zur Deckung gebracht
werden; oder, bei der das Objekt und sein Abbild nach ihren Maßen und ihrer
Lage ununterscheidbar sind.
In der Symmetrielehre wird unsere Definition in der Regel ganz naiv auch auf Objekte der realen Welt angewendet. Wir wollen dies hinterfragen. In den exakten Naturwissenschaften werden die Objekte der realen Welt durch physikalische oder chemische Modelle (Molekülmodelle, Modelle von Kristallen) dargestellt. Auf diese Modelle lässt sich unsere Definition tatsächlich ohne Problem ausdehnen. Dagegen besitzen die Objekte der realen Welt in Form und Aufbau Unvollkommenheiten: Sie sind streng genommen niemals symmetrisch.
Definition
Ein Symmetrielement (SE) ist ein geometrisches Objekt, welches bei der
zugehörigen Symmetrieoperation unverändert bleibt.
Die Idee der Symmetrieelemente ist sehr anschaulich, wie man gleich an den Beispielen sehen wird. Alle elementaren Beschreibungen von Symmetrie gehen deshalb von Symmetrieelementen aus. Dagegen verwendet die mathematische Behandlung der Symmetrie die abstrakteren Symmetrieoperationen. Es ist nicht zufällig so, dass unsere Definition einer Symmetrieoperation scharf ist, während der Begriff des Symmetrieelements eher unscharf bleibt. Tatsächlich gibt es eine kontroverse Diskussion über die Definition und Bedeutung von Symmetrieelementen. Wir wollen uns damit aber nicht aufhalten. Vielmehr wollen wir im Folgenden an Hand einiger Beispiele unser Verständnis entwickeln und neue Begriffe einführen.
Wir nehmen als erstes Beispiel das Molekül BF3. Man kann das BF3-Molekül um eine Achse drehen, die durch das B-Atom geht und senkrecht auf der Molekülfläche steht. Drehungen um 120° und um 240° bringen das Molekül mit sich zur Deckung, sind also Symmetrieoperationen. Die Drehachse bleibt bei der Drehung unverändert, ist also das zugehörige Symmetrieelement.
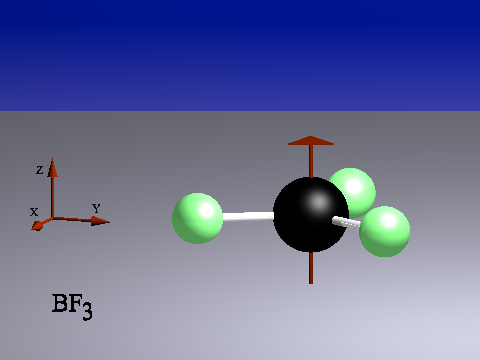
Neben den Drehungen um 120° und 240° sind alle Drehungen
möglich, die ganzahlige Vielfache von 120° sind. Darunter ist die
triviale Symmetrieoperation oder Einheitsoperation, hier die Drehung
um 0°, das "in Ruhe lassen". Eine Drehung um 360° bewirkt
das Gleiche wie eine Drehung
um 0° und wird deshalb als nicht verschieden angesehen. Ganz analog wird
auch eine Drehung um 480° als nicht verschieden von einer Drehung um
120° angesehen. Wir nennen eine solche Drehachse dreizählig und
verwenden für sie das Symbol C3. Der zugehörige
Drehwinkel ist 2π/3 = 120°. Die
zugehörigen Symmetrieoperationen bezeichnen wir mit den kursiven Symbolen
E, C3, C32
mit C33 = E.
Hier noch ein paar einfache Ergänzungen.
1. Das BF3-Molekül besitzt noch drei zweizählige
Drehachsen, die in der Ebene des Moleküls liegen.
2. Das Molekül CO besitzt eine unendlich-zählige Drehachse
Cn mit n = unendlich. Der zugehörige Drehwinkel ist beliebig und
kann auch infinitesimal sein.
In unserem ersten Beispiel für Spiegelsymmetrie betrachten wir ein Wasser-Molekül H2O. Wir erkennen eine zweizählige Drehachse C2; eine Drehung um 180° vertauscht die beiden H-Atome. In der Abbildung haben wir die Drehachse, einer allgemeinen Konvention folgend, senkrecht gestellt. Das Molekül besitzt ferner zwei vertikal stehende Spiegelebenen σv und σv', deren Schnittline mit der Drehachse zusammenfällt. Die erste enthält das Molekül. Die zweite steht senkrecht dazu. Eine Spiegelung an dieser zweiten Spiegelebene vertauscht die beiden H-Atome.
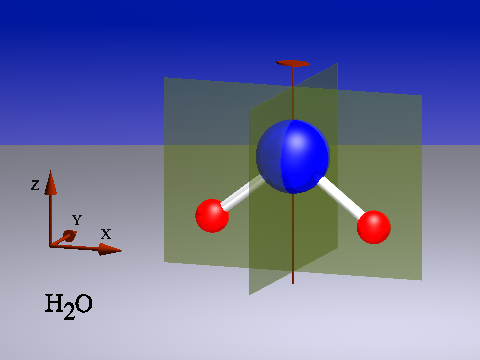
Die Wirkung der Symmetrieoperationen kann man auch wie folgt beschreiben. Die Drehung vertauscht rechts und links und gleichzeitig vorn und hinten. Die eine Spiegelung vertauscht rechts und links, die andere vorn und hinten. Sehr schön kann man den Unterschied auch an einem orthogonalen Achsensystem (x,y,z) sehen. Eine Drehung um die z-Achse führt von einem Punkt P(x,y,z) zu einem Punkt P'(-x,-y,z) mit einem Vorzeichenwechsel der x- und y-Koordinaten. Eine Spiegelung an der xz-Ebene kehrt das Vorzeichen der y-Koordinaten um, eine an der yz-Ebene das Vorzeichen der x-Koordinaten.
In unserem zweiten Beispiel für Spiegelsymmetrie betrachten wir das (E)-1,2-Dichlorethen-Molekül. Das Molekül ist planar. Durch den Mittelpunkt des Moleküls gibt es eine zweizählige Drehachse C2, die senkrecht auf der Molekülebene steht. Wir stellen die Drehachse konventionsgemäß senkrecht. Die Molekülebene steht jetzt horizontal. Sie ist trivialerweise eine Spiegelebene und wird als σh bezeichnet.
Unser Beipielmolekül besitzt - und das ist das eigentlich Neue des Beispiels - ein Symmetriezentrum i als Symmetrieelement, in der Abb. als Ring um den Schnittpunkt von Drehachse und Spiegelebene angedeutet. Die zugehörige Symmetrieoperation ist die Inversion i. Bei der Zentrosymmetrie gibt es zu jedem Atom außerhalb des Symmetriezentrums ein "gegenüber" liegendes Atom. Im orthogonalen Achsensystem wechseln alle drei Koordinaten des Atoms das Vorzeichen, wenn man zum Atom gegenüber übergeht..
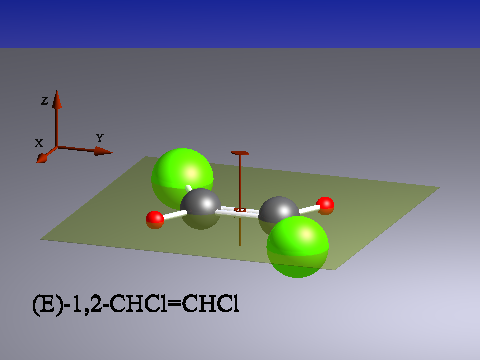
Wir können aufgrund der gewonnenen Einsichten zwei wichtige
Feststellungen treffen.
1. Zwischen Rotations- und Spiegelsymmetrie besteht ein
grundsätzlicher Unterschied: Drehungen sind im physikalischen Raum
tatsächlich ausführbar, Spiegelungen sind nur gedanklich
möglich.
2. Wir haben zwei verschiedene Arten von
Spiegelsymmetrie:
– Spiegelungen an einer Spiegelebene; alle Punkte
der Spiegelebene bleiben bei der Spiegelung erhalten.
– Spiegelungen am so genannten Symmetriezentrum;
bei der Inversion bleibt nur ein Punkt, nämlich das Symmetriezentrum,
erhalten.
Wenn wir eine rechte Hand in einem (ebenen) Spiegel betrachten, sehen wir im
Spiegel eine linke Hand als Spiegelbild. Es gibt nun zwei ganz
verschiedene Weisen, diese Situation zu interpretieren.
1. Eine einzelne Hand ist ein unsymmetrisches Objekt. Die Spiegelebene dient
dazu, die Operation der Spiegelung zu ermöglichen. Sie ist hier kein
Symmetrieelement; auch ist die Operation der Spiegelung keine
Symmetrieoperation.
2. Das Paar von rechter und linker Hand zusammen (Abb.) ist spiegelsymmetrisch. Die Spiegelebene ist jetzt
Symmetrieelement.
übrigens: Unser eigenes Paar Hände ist nur in der beschriebenen
Aufstellung symmetrisch. Wenn
wir eine der beiden Hände drehen, geht die Spiegelsymmetrie verloren.
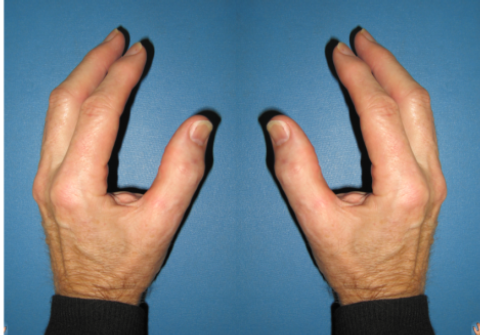
Was wir hier am Beispiel der Hände gesehen haben, können wir in die Welt der Moleküle übertragen. Der einzelnen Hand entspricht das chirale Molekül.
Definition
Ein Objekt (Alltagsobjekt, Molekül, Kristall) heißt chiral, wenn sein Bild
von seinem Spiegelbild verschieden ist, d.h. wenn sein Bild mit seinem
Spiegelbild nicht mit Hilfe von Verschiebungen und äußeren
Drehungen zur Deckung gebracht werden kann. Das Objekt kann dann in zwei enantiomeren Formen existieren, die sich zueinander wie Bild und
Spiegelbild verhalten.
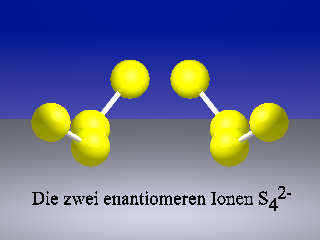
Als erstes Beispiel betrachten wir die Tetrasulfid-Ionen S42-, die man in kristallinen Alkalimetall-tetrasulfiden antrifft. Die Tetrasulfid-Ionen sind wie die geläufigeren Moleküle H2O2 und H2S2 nicht planar. Aus der Abbildung sieht man, dass sie eine zweizählige Drehachse besitzen. Es gelingt aber nicht, sie durch eine äußere Drehung miteinder zur Deckung zu bringen. Tetrasulfid-Ionen sind also chiral, aber nicht unsymmetrisch. Wenn man die beiden Molekülhälften um die mittlere S-S-Bindung gegeneinder verdreht, ist das eine interne Rotation; diese überführt ein Enantiomer in das andere. Aus diesem Grund ist in der obigen Definition von "äußeren Drehungen" und nicht einfach von Drehungen die Rede.
Das Beispiel zeigt uns, dass ein chirales Molekül (oder Ion) aus mindestens vier Atomen bestehen muss. Dreiatomige Moleküle sind planar und damit notwendig spiegelsymmetrisch; erst durch das Hinzufügen eines vierten Atoms kann die Spiegelebene zerstört werden. Es zeigt uns weiter: Chirale Moleküle können Drehsymmetrie besitzen.
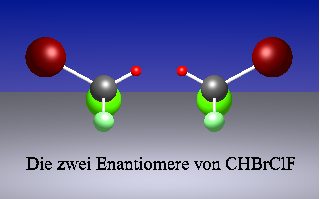
Die einfachsten chiralen organischen Verbindungen sind Methan-Derivate mit vier verschiedenen Substituenten am zentralen Kohlenstoff-Atom. Als Beispiel nehmen wir ein Bromchlorfluormethan CHBrClF. Die Abbildung zeigt die beiden enantiomeren Formen des Moleküls. Die vier Substituenten besetzen jeweils die Ecken eines Tetraeders, in dessen Innerem das C-Atom liegt. Die einfachsten biochemisch interessanten Beispiele sind deutlich komplizierter; auf sie kommen wir deshalb erst später.
Eine ganz andere Art von Symmetrie finden wir in einem Bandornament. Wir sehen ein Motiv, das sich in regelmäßigen Abständen wiederholt. Durch Verschieben des Bandornaments kann man das Motiv mit einer seiner Wiederholungen zur Deckung bringen. Das Verschieben kann um eine kleinste Strecke t erfolgen oder ebenso gut um ganzzahlige Vielfache von t. Das Verschieben ist jedoch keine Symmetrieoperation: Es wird zwar das Motiv mit sich selbst zur Deckung gebracht, aber an beiden Enden kommen das ursprüngliche und das verschobene Bandornament nicht zur Deckung.

Wir idealisieren nun unser Bandornament, indem wir annehmen, dass es in der Richtung der Verschiebung unendlich ausgedehnt sei. Es gibt dann keine störenden Enden mehr. In der Sprache der Symmetrielehre haben wir einen Elementarbereich, aus dem durch translatorische Wiederholung das gesamte Ornament erzeugt werden kann.
Der Elementarbereich ist allgemein ein Parallelogramm. Die Wahl des Elementarbereichs ist übrigens weitgehend willkürlich. Das demonstrieren die beiden folgenden Beispiele: ein Parallelogramm und ein Rechteck (das Rechteck ist ein spezielles Parallelogramm, nämlich eines mit rechten Winkeln).

Der Elementarbereich wird in der Regel kleinstmöglich gewählt und enthält (wie in beiden Beispielen) das Motiv genau einmal. Ein solcher kleinstmöglicher Elementarbereich heißt primitiv.
Die Translation um t und Translationen um ganzzahlige Vielfache davon sind beim unendlich langen Bandornament Symmetrieoperationen. Ein Symmetrieelement zur Translation gibt es nicht, denn es gibt keine Punkte im Raum, die bei einer Translation unverändert bleiben. Translationen werden mathematisch durch Vektoren dargestellt; Vektoren haben eine Richtung und als Betrag eine Länge.
Einige Ergänzungen:
1. Indem wir ein Bandornament auf einen Elementarbereich und translatorische
Symmetrie zurückführen, leisten wir gedanklich eine enorme und
grundlegende Abstraktion.
2. Beim endlich langen Bandornament zerstören die beiden Enden die
translatorische Symmetrie. Wir nennen das Symmetriebrechung.
3. Translatorische Wiederholung kann in mehr als einer Richtung möglich
sein. In ebenen Mustern, also in Mustern von Tapeten und Textilien, liegt
translatorische Symmetrie in zwei unabhängigen Raumrichtungen vor; dabei
sind die Muster zweidimensional unendlich ausgedehnt zu denken. In
klassischen Kristallen liegt translatorische Symmetrie in drei unabhängigen
Raumrichtungen vor; der Idealkristall ist
dreidimensional unendlich ausgedehnt.
4. Reale Kristalle im Labor haben Kantenlängen in der
Größenordnung von einem Millimeter. Längs der Kanten
wiederholt sich eine bestimmte Anordnung von Atomen etwa eine Million Mal.
Bei der Idealisierung wird vernachlässigt, dass an den beiden
Kantenenden ein Fehler auftritt, nämlich dass die Wiederholung abgebrochen wird.
Anders ausgedrückt: Der Idealkristall ist ein gutes
Modell für den Realkristall. Man darf nur nicht übersehen,
dass dabei alle Oberflächenphänomene
unbeachtet bleiben.
Die vorangegangenen Beispiele haben uns gezeigt: Bei Dreh- und Spiegelsymmetrien gibt es mindestens einen Punkt, der seine Lage im Raum nicht ändert. Solche Symmetrien heißen Punktsymmetrien. Das Gegenstück hierzu bilden die translatorischen Symmetrien; sie heißen auch Raumsymmetrien. Raum meint hier nicht nur den physikalischen, dreidimensionalen Raum, sondern - abstrakter - einen ein-, zwei- oder dreidimensionalen (und in der Mathematik allgemein einen n-dimensionalen) Raum.
Der Gegensatz von Punktsymmetrie und Raumsymmetrie ist ein erster Ansatz zur Klassifizierung von Symmetrie. Im SMX-Projekt konzentrieren wir uns zunächst auf Moleküle und andere endliche Objekte, die alle eine Punktsymmetrie besitzen. Erst wenn wir die Punktsymmetrien sicher beherrschen, wenden wir uns den Kristallen und anderen unendlichen Objekten zu, um deren komplexere Raumsymmetrien kennen und verstehen zu lernen.