![]() Zum Inhaltsverzeichnis
Zum Inhaltsverzeichnis
![]() Zurück zum Haupttext
Zurück zum Haupttext
Man konstruiert ein Stereogramm, welches alle gegebenen Symmetrieelemente
berücksichtigt. Danach sucht man zusätzliche Symmetrieelemente.
Bei jeder Drehachse prüft man, ob eine Drehspiegelachse vorliegt, die
mit der Drehachse koinzidiert.
1. Symmetriezentrum i.
2. Dreizählige Drehspiegelachse S3.
3. Symmetriezentrum i und Drehspiegelachse S2n mit n
> 1. Im Fall n = 1 sind das Symmetriezentrum und die
Drehspiegelachse S2 identisch. Dieser hier ausgeschlossene
Sonderfall ist bereits unter 1. angesprochen.
Übung 1
Mögliche Erzeugende sind:
C2h = [C2, σh];
C2h = [C2, i];
C2h = [σh, i].
Übung 2
Stellt eine Untergruppe eine Erzeugende dar?
1. Alle Produkte und Potenzen von Elementen der Untergrupe sind
definitionsgemäß ebenfalls in
der Untergruppe. Wenn die Untergruppe eine eigentliche Untergruppe ist,
enthält die Gruppe weitere Elemente, die nicht in der Untergruppe
enthalten sind. Diese Elemente können, wie soeben fest gestellt, nicht
als Produkte von Elementen
der Untergruppe ausgedrückt werden.
2. Im Fall der Gruppe C1 = { E } hat man die
triviale Erzeugende
C1 = [E].
Diese Gruppe ist auch die einzige, deren Erzeugende das Einselement
enthält.
3. Die Erzeugende einer Gruppe, ausgenommen die Gruppe C1,
darf das Einselement nicht enthalten, denn definitionsgemäß muss
die Menge der Elemente in der Erzeugenden kleinstmöglich sein.
Übung 1
Ein Molekül der Punktgruppe C1 darf nicht planar sein
und muss aus wenigstens vier Atomen bestehen. Wir haben vieratomige
Moleküle wie H2O2 als typische Beispiele der
Punktgruppe C2 erwähnt. Diese Moleküle besitzen
unsymmetrische Isotopomere wie HDO2 oder
H216O18O.
Übung 2
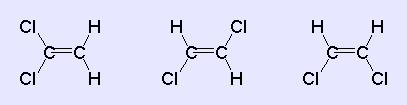
Die Punktgruppen sind
C2v für 1,1-Dichlorethen, mit der z-Achse in der
C–C-Bindung;
C2h für (E)-1,2-Dichlorethen;
C2v für (Z)-1,2-Dichlorethen, mit der z-Achse
senkrecht zur C–C-Bindung.
Übung 3
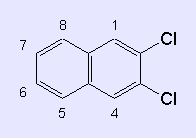
Die Punktgruppe der Stammverbindung Naphthalin ist D2h.
Das Numerierungsschema entnimmt man der unten gezeigten Formel des
2,3-Dichlornaphthalins. Als Symmetrien kommen die Untergruppen von
D2h in Frage, bei denen die
Molekülebene als Spiegelebene berücksichtigt ist:
- Cs für 1,2-, 1,3-, 1,6- und 1,7-Dichlornaphthalin;
- C2v für 1,4-, 1,8-, 2,3- und 2,7-Dichlornaphthalin;
- C2h für 1,5- und 2,6-Dichlornaphthalin.
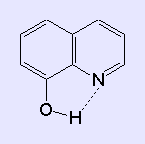
Übung 4
Zur Erinnerung: die Formel des 8-Hydroxychinolins.
Zum Aluminiumoxinat: Die Koordinationszahl des Aluminiums ist sechs. Das Anion
ist ein (O,N)-Ligand. Es gibt zwei Möglichkeiten:
1. Die drei N-Atome können facial angeordnet sein und besetzen
zusammen genau eine Dreiecksfläche (Abb. links). Die drei O-Atome sind dann
ebenfalls facial angeordnet und besetzen die entgegengesetzte
Dreiecksfläche. Die Symmetrie ist C3. Die Verbindung
ist chiral und existiert als Enantiomerenpaar.
2. Die drei N-Atome können meridional (wie auf einem Meridian)
angeordnet sein. Die Besetzung aller Dreiecksflächen ist gemischt, z.B.
soll die vordere Dreiecksfläche die Kombination N2O
aufweisen (Abb. rechts). Die hintere Dreiecksfläche hat dann die Kombination
NO2. Die Punktgruppe ist C1. Auch diese Verbindung
existiert als Enantiomerenpaar.
3. Es gibt keine weiteren Möglichkeiten. Erstens sind alle Kombinationen
NnO3-n bedacht. Zweitens gibt es bei Komplexen des
Typs MA3B3 genau zwei Isomere, das fac- und das
mer-Isomer. Wir kommen zweimal zum gleichen Schluss.
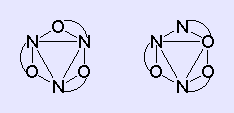
Übung 1
1. Planare Moleküle:
D4h für XeF4;
D2h für Naphthalin und 1,4-Dichlorbenzol;
2. Zwei wichtige Beispiele für Dnd-Symmetrie:
D3d für Cyclohexan in der Sesselform;
D4d für Cyclooctaschwefel S8;
3. Bipyramidale Moleküle:
D3h für PF5;
D5h für IF7;
4. Zwei einfache Metallcarbonyle:
D3h für Fe(CO)5, wie PF5;
D3h für Fe2(CO)9;
5. Zweimal Oktaedersubstitution:
D4h für trans-[OsCl4I2]2-;
D3 für [Tri(oxalato)chromat]3-, eine
chirale Spezies;
6. Ein zweiflügeliger Propeller:
D2d für Allen C3H4.
Übung 2
Bis(butan-2,3-diondioximato)nickel
1. D2h für die Struktur mit zwei symmetrischen (also
besonders starken) H-Brücken; die Anionenladung ist stark delokalisiert.
2. Unsymmetrische H-Brücken sind mit Erniedrigung der Symmetrie
verbunden; möglich sind im Prinzip alle Untergruppen von
D2h. Die Struktur mit zwei Monoanionen und der Symmetrie
C2h ist energetisch günstig.
Übung
1. Gruppe Oh, Beispiel des Oktaeders. Man kann das
Oktaeder auf sechs Flächen stellen und dabei jeweils eine von drei
Ecken in eine ausgwählte Position bringen. Es gibt also 24
symmetrieäquivalente Aufstellungen.
Demnach besteht die Drehgruppe O aus 24 Symmetrieoperationen. In der
Gruppe Oh kommen zu den 24 Drehungen noch 24
Drehspiegeloperationen hinzu.
2. Gruppe Td, Beispiel des regulären Tetraeders. Es
gibt vier Flächen mit je drei Ecken. Die Drehgruppe T besteht aus
12 Drehungen, die Gruppe Td aus 12 Drehungen und 12
Drehspiegelungen.
3. Gruppe C5v, Beispiel der fünfseitigen Pyramide.
Es ist neu an diesem Beisiel, dass die Pyramide zwei verschiedene Arten von
Flächen hat.
- Wir stellen die Pyramide auf die Basisfläche. Es gibt fünf
symmetrieäquivalente Aufstellungen. Jede dieser Aufstellungen
kann aus einer bestimmtem dieser Aufstellungen durch eine Drehung erreicht
werden. Die Drehgruppe C5 besteht also aus 5 Drehungen, die
Gruppe C5v aus 5 Drehungen und 5 Drehspiegelungen.
- Das Gleiche findet man, wenn man die Pyramide auf eine Seitenfläche
stellt. Aber Vorsicht: Keine
der Aufstellungen auf der Basisfläche kann durch eine
Symmetrieoperation in eine der Aufstellungen auf einer Seitenfläche
überführt werden. Man darf also nicht blindlings sagen, wir
hätten zweimal 5 Aufstellungen, also 10 Drehungen.
- Wir können auch ein Stereogramm konstruieren. Ein Punkt in
allgemeiner Lage ist in der Gruppe C5
fünfzählig, in der Gruppe C5v 10-zählig.
Diese Art, die Anzahl der Symmetrieoperationen einer Gruppe, zu bestimmen,
ist besonders bei niedriger Symmetrie praktisch.
4. Gruppe D5h, Beispiel der fünfseitigen Bipyramide.
Wir folgen hier dem Beispiel 3. Es gibt 10 Aufstellungen entsprechend den 10
Außenflächen. Die Gruppe D5 besteht aus 10
Drehungen, die Gruppe D5h aus 10 Drehungen und 10
Drehspiegeloperationen. Ein Punkt in allgemeiner Lage ist bei der
Punktgruppe D5 10-zählig, bei der Punktgruppe
D5h 20-zählig.
Übung 1
– Quader: E = 8, F = 6, K = 12; 8 - 12 + 6 = 2;
– vierseitiges Prisma: wie beim Quader! Wenn man einen Würfel
längs der vierzähligen Drehachsen dehnt oder staucht, kommt man zu
niedrigeren Symmetrien, konkret zum vierseitigen Prisma und zum Quader; die
Zahl der Ecken, Flächen und Kanten ändert sich dabei nicht.
– vierseitige Bipyramide: E = 6, F = 8, K = 12;
6 - 12 + 8 = 2 ; Dehnung oder Stauchung eines regulären Oktaeders
längs einer der vierzähligen Drehachsen ergibt vierseitige
Bipyramiden.
– trigonales Antiprisma: wie bei der vierseitigen Bipyramide! Trigonale
Antiprismen erhält man durch Dehnung oder Stauchung eines
regulären Oktaeders längs einer der dreizähligen Drehachsen.
Übung 2
1. 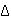 E = - 1 + 3 = 2;
E = - 1 + 3 = 2;
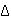 F = 1;
F = 1;
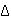 K = 3.
K = 3.
Der Eulersche Polyedersatz gilt vor und nach dem Abschneiden der Ecke. Daher
muss gelten:
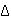 E -
E - 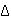 K +
K +
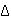 F = 0
F = 0
2. 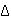 E = - 1;
E = - 1;
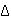 F = 1;
F = 1;
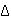 K = 3 - 3 = 0.
K = 3 - 3 = 0.
Auch hier ist die Summe der Änderungen gleich Null.
Übung 1
Bei dieser Aufgabe entdecken Sie eine Vielfalt von Situationen. Wir machen
zunächst einige Bemerkungen zu den Flächen. Beim
Würfel sieht man längs einer C3--Achse ein reguläres
Sechseck mit drei, das heißt der Hälfte der Flächen. Alle
Platonischen Körper haben eine derartige Projektionsrichtung; besonders
schön ist beim Pentagondodekaeder das reguläre Zehneck mit 6 von
zwölf Flächen, welches man längs der C5-Richtung
sieht. Dann gibt es
die schwierigeren Projektionsrichungen, bei denen Flächen zu Linien
reduziert sind. Beim Würfel sind längs einer C2-Achse
zwei Flächen auf der Vorderseite sichtbar, zwei entsprechende auf der
Rückseite nicht sichtbar und je eine weitere rechts und links zu einer
Linie reduziert. Die Projektion längs der C2-Achse zeigt
beim Pentagondodekaeder und beim Ikosaeder sogar 4 Flächen als
Begrenzungslinien der Figur.
Die Zahl der Ecken und Kanten läßt sich jetzt ganz leicht herausfinden. Wenn das Polyeder von k n-Ecken umgrenzt wird, ist die Zahl der Kanten kn/2; jede Kante gehört ja zu zwei Polygonen. Wenn an einer Ecke m n-Ecke zusammentreffen, ist die Zahl der Ecken kn/m. In den Ansichten sieht man mindestens die Hälfte der Ecken und Kanten. Das Abzählen bleibt aber meist mühsam und ist fehleranfällig.
Übung 2
Würfel: C2v und D2h, C3v
und D3d.
Oktaeder: C2v und D2h, C3v und
D3d, C4v und D4h.
Tetraeder: C2v und D2d,
C3v.
Ikosaeder und Pentgondodekaeder: C2v und
D2h, C3v und D3d,
C5v und D5d.
Anmerkung: Die erste Nennung bezieht sich auf die Ansicht von vorn, die
zweite berücksichtigt auch die Hinterseite. Die Liste ist keineswegs
vollständig. Z.B. ist C3 eine Untergruppe von
C3v und (nicht ganz so trivial) S4 eine
Untergruppe von D2d.
Übung 1
1. Der resultierende Archimedische Körper wird von vier gleichseitigen
Dreiecken und vier regelmäßigen Sechsecken umgrenzt. Seine
Kantenläge ist a/3.
2. F = 4 + 4 = 8; E = 4 × 3 = 12; K = 4 × 3
+ 6 = 18.
3. Denkbar ist ein gespannter Kohlenwasserstoff der Formel
C12H12.
4. Übrig bleibt ein reguläres Tetraeder.
Übung 2
1. Punktgruppe D3h.
2. Dieses spezielle trigonale Prisma ist semiregulär, aber kein
Archimedischer Körper.
Nur die hochsymmetrischen, semiregulären Körper werden als
Archimedische Körper bezeichnet.
3. Der gespannte Kohlenwasserstoff Prisman C6H6 mit
drei Dreiringen und drei Vierringen ist bekannt.
Übung 1
Die Struktur des Moleküls Zn4O(CH3CO2)6
muss ein-, vier- und sechszählige Lagen besitzen, was auf einen
regulär tetraedrischen Bau hinweist. Sie kann durch die Formel
Zn4(µ4-O)(µ-CH3CO2)6
beschrieben werden. Im Zentrum eines Zn4-Tetraeders befindet sich ein vierfach
verbrückender Oxid-Ligand; die sechs Tetraederkanten sind durch
Acetat-Liganden überbrückt. Die Punktgruppe ist
Td.
Übung 2
Folgende Chlor-Derivate des Kubans sind möglich.
1. 1,2,3,8-Tetrachlorkuban mit der Symmetrie C4v.
2. Es gibt folgende Derivate:
– 1-Chlorkuban mit der Symmetrie C3v;
– 1,3,5-Trichlorkuban mit der Symmetrie C3v;
– 1,2,3,5-Tetrachlorkuban mit der Symmetrie C3v;
– 1,3,5,7-Tetrachlorkuban mit der Symmetrie Td;
– 1,2,3,5,7-Pentachlorkuban mit der Symmetrie C3v;
– 1,2,3,4,5,6,7-Heptachlorkuban mit der Symmetrie C3v.
Hinweis: Wenn man den Würfel so aufstellt, dass eine
C3-Achse senkrecht steht, kann man die Ecken in vier Etagen mit
1, 3, 3 und 1 C-Atomen einteilen. Die Ecken einer Etage müssen entweder
alle unsubstituiert sein oder alle substituiert; nur so kann die
C3-Achse bestehen bleiben.
Übung 3
Urotropin
1. Punktgruppe: Td.
2. Es gibt keine Atome in allgemeiner Lage.
3. In den Ecken sind dreibindige Gruppen wie CH und N möglich, in den
Brückenpositionen zweibindige Gruppen wie CH2, O und S.
Typische Vertreter sind Adamantan C10H16 =
(CH)4(CH2)6
und die Phophor-Verbindungen P4O6
("Phosphortrioxid"), P4O10
(die molekular gebaute Modifikation von "Phosphorpentoxid")
und P4S10 ("Phosphorpentasulfid").
Übung 4
Co6(CO)16 =
Co6(µ3-CO)4(CO)12, ebenso
der entsprechende Rhodium-Komplex
Punktgruppe: Td.
Übung 5
Dehnung oder Stauchung
1. längs einer C4-Achse: Punktgruppe
D4h;
2. längs einer C3-Achse: Punktgruppe
D3d;
3. längs einer C2-Achse: Punktgruppe
D2h.
Übung 6
Man muss die Spiegelebenen zerstören und dabei die Drehachsen erhalten.
Das erreicht man, indem man alle acht Dreiecksflächen um den gleichen
Winkel verdreht. Man kann sich z.B. ein Modell vorstellen, bei dem die
Dreiecksflächen auf die dreizähligen Achsen aufgesteckt sind und
nicht miteinander fest verbunden sind.
Übung 1
Folgende Punktgruppen werden innerhalb einer Drehung um 72°
durchlaufen: D5h (bei 0°), D5,
D5d (bei 36°), wieder D5 und
schließlich D5h (bei 72°).
Übung 2
Die Punktgruppen sind: bei 0° D2h, bei 30° und
45° D2
und bei 90° D2d. Sie haben sich vielleicht durch die
45° kurz irritieren lassen; jetzt ist aber klar, dass bei allen Winkeln
außer exakt 0, 90, 180 oder 270° die Punktgruppe
D2 vorliegt.
Der Torsionswinkel von 0° entspricht der Rotationsstellung "auf
Deckung". Man blickt längs der Längsachse des Biphenyls; die
beiden Phenyl-Ringe sind koplanar. Der Torsionswinkel von 90° entspricht
der Rotationsstellung "auf Lücke".
Die Aufgaben 1 und 2 sind
völlig analog. Die Dnd-Symmetrie wird jeweils bei
einem Torsionswinkel von 360 / 2n° erreicht.
Übung 3
1. Bei einem Torsionswinkel von 0° sind die Punktgruppen
Cn und Cnv möglich, wenn alle
Methyl-Gruppen die gleiche Rotationsstellung bezüglich der
C5-Ebene des Cp*-Rings haben. Bei der höheren
Cnv-Symmetrie
müssen alle Methyl-Gruppen auch die vertikalen Spiegelebenen wahren;
anschaulich heißt das, dass bei allen Methyl-Gruppen jeweils ein H-Atom
zum Metall hin gerichtet ist oder alternativ dass bei allen Methyl-Gruppen
jeweils ein H-Atom vom Metall weg gerichtet ist.
2. Bei einem Torsionswinkel von 10° kann die Symmetrie nur niedriger
als im ersten Fall sein. Die Punktgruppe Cn liegt vor, wenn
alle Methyl-Gruppen die gleiche Rotationsstellung bezüglich der
C5-Ebene des Cp*-Rings haben. Andernfalls ist die Punktgruppe nur
noch C1.