2.3. Punktgruppen: Begriffe, Ideen, Beispiele

Teil von  Zum Inhaltsverzeichnis

nach unten 2.3.1. Kombination von Symmetrieelementen
nach unten 2.3.2. Erzeugende einer Punktgruppe
nach unten 2.3.3. Die Aufzählung der Punktgruppen
nach unten 2.3.4. Punktgruppen mit höchstens einer Dreh- oder Drehspiegelachse
nach unten 2.3.5. Diedergruppen
nach unten 2.3.6. Hochsymmetrische Punktgruppen
nach unten 2.3.7. Punktgruppen und interne Rotation

nach unten

Ein zentrales Thema der Symmetrielehre ist die systematische Aufzählung aller möglichen Punktgruppen. Wir behandeln dieses Thema in zwei Kapiteln.
1. In vorliegenden Kapitel lernen wir neue Ideen und Begriffe kennen und entwickeln unsere Anschauung mit Hilfe von Beispielen und Übungen. Zusätzliche Einzelheiten und technische Details findet man über Verweise.
2. in einem knapp gehaltenen, zweiten Kapitel listen wir die möglichen Punktgruppen auf. Dort steht die Systematik im Vordergrund.

Die beiden Kapitel sind in Teilen parallel und sollten auch parallel bearbeitet werden. Dazu gibt es die notwendigen Querverweise im Text.

2.3.1. Kombination von Symmetrieelementen

Zuerst brauchen wir den Begriff der Kombination von Symmetrieelementen. In einer gegebenen Symmetrie sind oft mehrere Symmetrieelemente kombiniert. Welche Kombinationen möglich sind, unterliegt Spielregeln. Wir machen uns das an einfachen Beispielen deutlich.
1. Ein Symmetrieelement vervielfacht ein anderes durch symmetrische Wiederholung. Beipielsweise hat man im BF3 eine C3-Achse und senkrecht dazu drei C2-Achsen.
2. Zwei Symmetrieelemente erzwingen oft die Anwesenheit eines dritten. Beispielsweise hat man im H2O-Molekül zwei sich schneidende (vertikale) Spiegelebenen; die Schnittlinie ist eine C2-Achse. Siehe dazu weiter unten den Verweis.
3. Kombinationen von Symmetrieelementen können auch unmöglich sein. Beispielsweise können mehrere C4-Achsen bei einer Kugel beliebig kombiniert werden. Mehrere C4-Achsen können sonst nur in Form eines orthogonalen Dreibeins von drei C4-Achsen in der Symmetrie des Würfels auftreten.

Kapitel  Kombinationen von Spiegelebenen
Kapitel  Übungen

2.3.2. Erzeugende einer Punktgruppe

Ferner brauchen wir den Begriff der Erzeugenden einer Gruppe. Um diesen neuen Begriff zu erklären, gehen wir aus vom Beispiel einer Drehachse Cn mit den Drehungen Cn, Cn2, ..., Cnn = E. Die Menge der Potenzen des Symmetrieoperators Cn bildet eine Gruppe, die wir als Drehgruppe Cn bezeichnen. Wem dieser Schluss zu schnell ging, sollte sich Punkt für Punkt davon überzeugen, dass die Gruppenpostulate erfüllt sind. Wir sagen jetzt: Der Symmetrieoperator Cn ist die Erzeugende der Drehgruppe Cn. Als Symbol für Erzeugende verwenden wir eckigen Klammern und schreiben:

 Cn = [Cn] mit n = 1, 2, 3, ...

Bei den Drehgruppen umfasst die Erzeugende nur ein einziges Gruppenelement. Bei vielen Punktgruppen braucht man Erzeugende mit zwei oder drei Gruppenelementen. Damit können wir jetzt den Begriff der Erzeugenden definieren.

Definition
Als Erzeugende einer Punktgruppe bezeichnet man jede kleinste Menge von Symmetrieoperatoren, aus der durch Kombination, d.h. durch Bildung aller möglichen Produkte, die Gesamtheit der Symmetrieoperatoren der Punktgruppe erzeugt werden kann.

Das Wort "jede" in der Definition deutet an, dass es bei der Angabe einer Erzeugenden mehrere Möglichkeiten geben kann. Am Beispiel des Wasser-Moleküls haben wir gesehen, dass die beiden vertikalen Spiegelebenen des Moleküls als Schnittlinie eine zweizählige Drehachse haben. Als Erzeugende der Gruppe könnten wir die beiden Spiegelungen nehmen oder ebenso gut eine Drehung C2 und eine Spiegelung. Diese Wahlfreiheit ist eine weitere Quelle für Unterschiede zwischen dem Schoenflies- und dem Hermann-Mauguin-System.

Die Konstruktion der Stereogramme von Punktgruppen nimmt Bezug auf die Erzeugende der Gruppe. Man beginnt mit einem Punkt in allgemeiner Lage und lässt genau die Symmetrieelemente einwirken, von denen die entsprechenden Symmetrieoperatoren in der Erzeugenden auftreten.

Kapitel  Konstruktion von Stereogrammen
Kapitel  Übungen

2.3.3. Die Aufzählung der Punktgruppen

Unter Aufzählung der Punktgruppen versteht man erstens eine systematische Auflistung der Punktgruppen und zweitens den Beweis der Vollständigkeit der Auflistung. Dieses Thema ist formal anspruchsvoller. Wir bereiten die Auflistung hier mit Beipielen vor und verweisen für die Durchführung auf das Kapitel zur Systematik der Punktgruppen.

Kapitel  Die Aufzählung im Einzelnen

2.3.4. Punktgruppen mit höchstens einer Dreh- oder Drehspiegelachse

Die einfachsten Klassen von Punktgruppen sind die Gruppen, die durch eine Drehung erzeugt werden. Diese Gruppen werden von uns als 1. Klasse geführt. Die zugehörige Achse wird stets senkrecht gestellt; falls ein Achsensystem benötigt wird, legt man die Achse stets in z-Richtung. Weitere Punktgruppen werden erhalten, indem wir die Drehung auf verschiedene Weisen mit Spiegelungen kombinieren (2. - 5. Klasse). Aus der Sicht der Chemie sind die resultierenden Punktgruppen von ganz unterschiedlicher Wichtigkeit.

Gruppen mit einer Drehachse (1. Klasse)

Die Punktgruppen Cn sind bei der Erklärung des Begriffs der Erzeugenden schon beschrieben worden. Bei den Windrädchen der Kinder und bei den Propellern moderner Windkraftanlagen finden wir die Symmetrie C3. Historische Windmühlen haben Propeller mit C4-Symmetrie. In der organischen Stereochemie ist die Symmetrie C2 sehr wichtig; das kleinste Molekül mit dieser Symmetrie ist das H2O2. Als Beispiel der Symmetrie C3 nennen wir das Triphenylphosphan P(C6H5)3, welches in der Komplexchemie und Katalyse eine große Rolle spielt.

Kapitel  Beispiele: Körper mit Drehsymmetrie und nichts mehr
Kapitel  Beispiele: Moleküle mit Cn-Symmetrie

Gruppen mit einer Drehachse und vertikalen Spiegelebenen (2. Klasse)

Das Urbeispiel dieser Symmetrie ist das Wasser-Molekül mit seiner C2-Achse und seinen zwei vertikalen Spiegelebenen. Wir nennen diese Symmetrie C2v. Die C2v-Symmetrie ist überaus häufig. Deshalb finden es manche Studenten schwer einzusehen, dass die C2-Achse nicht mit vertikalen Spiegelebenen verbunden sein muss. Ein Vergleich der beiden Beispiele H2O und H2O2 sollte hilfreich sein.

Die charakteristischen Polyeder mit Cnv-Symmetrie sind die n-seitigen Pyramiden, für die die Cheops-Pyramide sicher das berühmteste Beispiel ist. Zahlreiche Moleküle besitzen eine C3v-Symmetrie, aber auch höhere Zähligkeiten der Drehachse kommen gelegentlich vor.

Kapitel  Beispiele: n-seitige Pyramiden
Kapitel  Beispiele: Moleküle mit Cnv-Symmetrie

Bei allen Molekülen der Punktgruppen Cnv ist die "obere" Hälfte verschieden von der "unteren". Diese Moleküle besitzen ein elektrisches Dipolmoment, oder kurz, sie sind polar. Eine Achse mit verschiedenen Enden heißt polar. Manchmal werden auch Punktgruppen, die ein elektrisches Dipolmoment erlauben, als polare Punktgruppen bezeichnet.

Gruppen mit einer Drehachse und einer horizontalen Spiegelebene (3. Klasse)

Sehr viel seltener findet man Moleküle, bei denen eine Drehachse mit einer horizontalen Spiegelebene kombiniert ist. Als Beipiel für die Punktgruppe C2h kann das (E)-1,2-Dichlorethen (E für 1,2-Anordnung "auf entgegengesetzten Seiten" der Doppelbindung) dienen und für die Punktgruppe C3h das Borsäure-Molekül.

Kapitel  Beispiele: Moleküle mit Cnh-Symmetrie

Gruppen mit einer Drehspiegelachse

Punktgruppen, die eine Drehspiegelung als Erzeugende haben, sind kompliziert und treten eher selten bei Molekülen auf. Deshalb wollen wir sie hier nur kurz und nur der Vollständigkeit halber streifen. Wer sich zum ersten Mal mit den Punktgruppen befasst, sollte sich hier nicht entmutigen lassen, sondern unbekümmert zum nächsten Gegenstand weitergehen.

1. Die Symmetrie des H3BO3-Moleküls enthält eine C3-Achse und eine horizontale Spiegelebene, also genau die Symmetrieoperationen, die man zu einer Drehspiegelung S3 zusammenfassen kann. Die Punktgruppe könnte S3 genannt werden. Im Schoenflies-System wird dem alternativen Namen C3h der Vorzug gegeben und die Gruppe unserer 3. Klasse zugeordnet.

2. Die Symmetrie, die mit Hilfe einer Drehspiegelachse S6 beschrieben werden kann (ohne dass noch andere Symmetrieelemente vorliegen), kann alternativ mit Hilfe einer C3-Achse und einem Symmetriezentrum i beschrieben werden. Auch hier vermeidet das Schoenflies-System das Punktgruppensymbol S6 und verwendet den alternativen Namen C3i unserer 4. Klasse. Einfache molekulare Beispiele gibt es nicht.

3. Bei den Gruppen S4, S8 usw. gibt es keine alternative Beschreibung; wir führen sie als 5. Klasse. Hier muss das Schoenflies-System notgedrungen Gruppensymbole verwenden, die von Drehspiegelungen abgeleitet sind.

Wir hatten im Kapitel über Drehspiegelungen bzw. Drehspiegelachsen bereits ausgeführt, dass es drei Arten von Drehspiegelachsen gibt. Ganz parallel dazu haben wir hier drei Klassen von Punktgruppen, die durch eine Drehspiegelung (und nichts mehr) erzeugt werden.

Vier Sonderfälle

1. Bei den reinen Drehgruppen Cn (1. Klasse) ist die Punktgruppe C1 ein Sonderfall. Bei einem Drehwinkel von 0° bleibt die Achsenrichtung undefiniert. Diese Punktgruppe hat nur eine Symmetrieoperation, nämlich C1 = E. Alle unsymmetrischen Objekte (Moleküle) haben die Punktgruppe C1; sie sind notwendig chiral. Man kann einfache Beispiele für diese Punktgruppe konstruieren wie unser früheres Beispiel CHDClF. Viel wichtiger ist aber, dass die natürlichen Aminosäuren außer Glycin, die meisten Zucker, die Steroide und viele andere Naturstoffe zu dieser Punktgruppe gehören und damit chiral sind.

2. Bei den Gruppen Cnv und Cnh verliert die Unterscheidung zwischen vertikal und horizontal für n = 1 ihren Sinn. Diese Punktgruppe wird mit Cs bezeichnet und hat als einzige nicht triviale Symmetrieoperation die Spiegelung an einer Ebene. Es gibt viele Moleküle mit Cs-Symmetrie. Dazu gehören planare Moleküle wie NOF, HCO2H, aber auch nicht planare Moleküle wie SOCl2, CH2ClI u.v.a.m.

3. Bei den Gruppen Cnv (2. Klasse) gibt es noch den Fall einer Drehachse der Zähligkeit unendlich, C∞. Alle axialsymmetrischen Objekte, deren "obere" und "untere" Hälften verschieden sind, besitzen die Punktgruppe C∞v. Dazu gehören z.B. der Kegel und im molekularen Bereich lineare Moleküle wie HD, HF, NO und HCN.

4. Bei den Gruppen Cni (4. Klasse) gibt es den Sonderfall n = 1. Hier bleibt die Achsenrichtung undefiniert und die möglichen Symmetrieoperationen sind E und i. Diese Punktgruppe heißt Ci. Sie spielt in der organischen Stereochemie eine wichtige Rolle. Es scheint aber kein einfaches, gut bekanntes, starres Molekül dieser Symmetrie zu geben.

Kapitel  Beispiele: Moleküle mit Ci-Symmetrie

Kapitel  Systematik dieser Punktgruppen
Kapitel  Übungen

2.3.5. Diedergruppen

Diedergruppen besitzen mehrere Achsen, aber höchstens eine mit einer Zähligkeit > 2. Die Achse höchster Zähligkeit n heißt Hauptachse; die Hauptachse wird stets senkrecht gestellt. Dazu gibt es noch n zweizählige Nebenachsen, die im rechten Winkel zur Hauptachse, also waagrecht stehen. Im einfachsten Fall gibt es nur Drehachsen (6. Klasse). Es kann aber auch zusätzliche Spiegelsymmetrie geben, die man in Form einer horizontalen Spiegelebene (7. Klasse) oder von diagonalen Spiegelebenen (8. Klasse) hinzufügen kann.

Diedergruppen mit einer horizontalen Spiegelebene (7. Klasse)

Unser früheres Beispiel BF3 ist typisch für Diedersymmetrie Dnh. Das Molekül besitzt eine dreizählige Hauptachse, senkrecht dazu drei zweizählige Nebenachsen, eine horizontale Spiegelebene (die Molekülebene), eine dreizählige Drehspiegelachse und drei vertikale Spiegelebenen. Seine Punktgruppe ist D3h.

Die charakteristischen Polyeder der Dnh-Gruppen sind die n-seitigen Prismen und die n-eckigen Bipyramiden. Im Fall der Gruppe D2h gibt es ein orthogonales Dreibein von zweizähligen Achsen; welche der drei Achsen als Hauptachse gewählt wird, ist willkürlich. Das Urbeispiel dieser Punktgruppe ist der Quader (Backstein, Streichholzschachtel).

Kapitel  Beispiele: Quader, Prismen, Bipyramiden
Kapitel  Beispiele: Moleküle mit Dnh-Symmetrie

Als Sonderfall gibt es noch die Punktgruppe D∞h. Dazu gehören alle axialsymmetrischen Objekte, deren "obere" und "untere" Hälften gleich sind, also z.B. der Zylinder und der Torus sowie im molekularen Bereich lineare Moleküle wie H2, CO2, HCCH und NCCN.

Diedergruppen mit diagonalen Spiegelebenen (8. Klasse)

Die Symmetrien Dnd findet man bei den n-seitigen Antiprismen und z.B. beim Dibortetrachlorid B2Cl4 und beim Allen C3H4 mit der Gruppe D2d, beim Cyclohexaschwefel S6 und beim Cyclohexan C6H12 jeweils mit der Gruppe D3d und beim Cyclooctaschwefel mit der Punktgruppe D4d. In der Gruppe D3d ist die allgemeine Punktlage 12-zählig. Beim Cyclohexaschwefel besetzen alle Atome eine spezielle Lage; beim Cyclohexan dagegen besetzen die H-Atome eine allgemeine Lage.

Kapitel  Beispiele: Bisphenoid und Antiprismen
Kapitel  Beispiele: Moleküle mit Dnd-Symmetrie

Diedergruppen ohne Spiegelsymmetrien (6. Klasse)

Bei den molekularen Beipielen dieser Klasse ist die Punktgruppe D3 wichtig. Es gibt hier zahlreiche chirale Tris(ligand)-Komplexe mit oktaedrischer Koordination des Zentralatoms wie z.B. das Tri(oxalato)chromat(III)-Ion [Cr(C2O4)3]3- und den Redoxindikator Ferroin [Fe(ophen)3]2+ (wo ophen für den planaren, zweizähnigen Liganden ortho-Phenanthrolin steht).

Kapitel  Beispiele: Tris(ligand)-Komplexe mit D3-Symmetrie

Kapitel  Systematik dieser Punktgruppen
Kapitel  Übungen

2.3.6. Hochsymmetrische Punktgruppen

Diedergruppen können eine Achse mit einer Zähligkeit > 2 besitzen. Es gibt nun noch einige faszinierende Punktgruppen, die mehrere Achsen höherer Zähligkeit besitzen (9. Klasse), nämlich:

 1. die Oktaedergruppen O und Oh;
 2. die Tetraedergruppen T, Td und Th;
 3. die Ikosaedergruppen I und Ih.

Die oktaedrische Symmetrie ist uns - zumindest in Teilen und vielleicht unbewusst - vertraut vom Würfel oder Kubus mit seinem orthogonalen Dreibein vierzähliger Achsen. In der tetraedrischen Symmetrie gibt es ein entsprechendes orthogonales Dreibein jetzt nur noch zweizähliger Achsen. Die beiden Symmetrien werden oft als kubische Symmetrie zusammengefasst. Deren Charakteristikum ist also das orthogonale Dreibein von mindestens zweizähligen Achsen.

Einige hochsymmetrische Polyeder stehen in enger Beziehung zu den hochsymmetrischen Punktgruppen. Sie sind einerseits ihre schönsten Realisierungen und haben andererseits die Phantasie der synthetischen Chemiker beflügelt. Wir befassen uns hier
- mit der Frage, wie man die Anzahl der Symmetrieoperationen komplizierter Gruppen am besten finden kann;
- mit dem Eulerschen Polyedersatz, den wir zur Beschreibung von Polyedern brauchen;
- mit den Platonischen Körpern und einigen Archimedischen Körpern.

Kapitel  Die Anzahl der Symmetrieoperationen einer Punktgruppe
Kapitel  Der Eulersche Polyedersatz
Kapitel  Die Platonischen Körper
Kapitel  Die Archimedischen Körper

In der Chemie sind die Gruppen Td und Oh sehr wichtig. Eine gewisse Bedeutung haben auch noch die Gruppen Th und Ih. Unter dem folgenden Verweis geben wir typische Beispiele, häufige und spezielle.

Kapitel  Beispiele: Hochsymmetrische Spezies

Kapitel  Systematik dieser Punktgruppen
Kapitel  Übungen

2.3.7. Punktgruppen und interne Rotation

In den vorangegangenen Abschnitten haben wir fast immer stillschweigend angenommen, dass Moleküle starr sind. Jedoch können bereits vieratomige Moleküle wie das H2O2 eine interne Rotation, d.h. eine Drehung der OH-Gruppen gegeneinander zeigen. Wir betrachten hier zuerst den einfacheren und besonders wichtigen Fall des Ethans C2H6.

Wir setzen das Ethan-Molekül aus zwei Methyl-Gruppen zusammen. Dabei können die beiden CH3-Gruppen relativ zueinander verschiedene Rotationsstellungen oder Konformationen einnehmen, und zwar
1. die ekliptische Stellung (Abb. links). Längs der C–C-Achse gesehen stehen die CH3-Gruppen zueinander auf Deckung; in dieser Konformation besitzt das Molekül die Punktgruppe D3h.
2. die gestaffelte Stellung (Abb. rechts). Längs der C–C-Achse gesehen stehen die CH3-Gruppen zueinander auf Lücke; in dieser Konformation besitzt das Molekül die Punktgruppe D3d.
3. die windschiefen Stellungen, d.h. alle Zwischenkonformationen. Die Symmetrie ist niedriger: Die Punktgruppe ist D3.

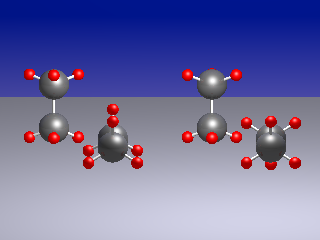
Ethan-Konformere

Die ekliptische Stellung und die gestaffelte Stellung sind spezielle Rotationsstellungen; die windschiefen Stellungen entsprechen dagegen der allgemeinen Rotationsstellung. Wegen der dreizähligen Achsensymmetrie des Ethans genügt es, Torsionswinkel zwischen 0 und 120° zu betrachten.

Die gestaffelte Konformation hat die niedrigste Energie, die ekliptische die höchste. Die Aktvierungsenergie für die Drehung der Methyl-Gruppen gegeneinander ist die Energiedifferenz zwischen der Energie der ekliptischen und der gestaffelten Konformation; sie heißt Barriere der internen Rotation. Im Fall des Ethans beträgt die Barriere etwa 12 kJ/mol. Das bedeutet einerseits, dass praktisch alle Moleküle in der gestaffelten Konformation vorliegen, andererseits aber auch, dass die interne Rotation bei Raumtemperatur schnell ist.

Um tiefer in diese Materie einzudringen, befassen wir uns
– mit dem Ethan-Molekül in mehr Detail;
– mit der internen Rotation des 1,2-Dichlorethans;
– und mit der inneren Beweglichkeit gesättigter Ringe.

Kapitel  Mehr zur internen Rotation des Ethans
Kapitel  Wir entdecken Konformationsisomerie: Das 1,2-Dichlorethan
Kapitel  Cyclohexan und Verwandte

Kapitel  Übungen

nach oben
E-Mail  smx-projekt@ac.rwth-aachen.de