![]() Zum Inhaltsverzeichnis
Zum Inhaltsverzeichnis
![]() Zurück zum Haupttext
Zurück zum Haupttext
Geschlossene, konvexe Polyeder mit Begrenzungsflächen aus regelmäßigen Vielecken sind im einfachsten Fall die Platonischen Körper, wenn nämlich nur eine Art von regelmäßigen Polygonen zugelassen wird. Wenn wir diese Einschränkung lockern und mehrere Arten von regelmäßigen, untereinander konkruenten Polygonen zulassen, gibt es weitere Klassen von Polyedern, die so genannten semiregulären Polyeder, darunter die meist hochsymmetrischen Archimedischen Körper. Reichlich Information hierzu findet man im Internet unter dem Suchwort "Archimedische Körper"; siehe insbesondere:
http://www.mathe.tu-freiberg.de/~hebisch/cafe/archimedische.html
http://www.dbilink.de/Archimedischer-Koerper.html
Definition
Ein geschlossenes, konvexes Polyeder heißt semiregulär, wenn
1. seine Oberfläche aus mehr als einer Art von regelmäßigen,
untereinander konkruenten Vielecken aufgebaut ist und wenn
2. jede seiner Ecken auf jede andere durch Symmetrieoperationen abgebildet
werden kann.
Ein semireguläres Polyeder heißt Archimedischer Körper, wenn es sich nicht um ein
Prisma oder ein Antiprisma handelt.
Unter den semiregulären Körpern gibt es:
1. Prismen mit quadratischen Seitenflächen und regelmäßigen
n-Ecken als Deck- und Bodenflächen. Sie haben die
Punktgruppen Dnh mit n = 3, 5, 6, ...; der Würfel
(n = 4) ist auszunehmen.
2. Antiprismen mit gleichseitigen Dreiecken als Seitenflächen und regelmäßigen
n-Ecken als Deck- und Bodenflächen. Sie haben
die Punktgruppen Dnd mit n = 4, 5, 6, ...; das
reguläre Oktaeder (n = 3) ist auszunehmen.
3. 13 Archimedische Körper, und zwar 11 achirale und 2 chirale, die
in zwei enantiomeren Formen konstruiert werden können.
Archimedes (287-212 v. Chr.) kannte offenbar
diese letztgenannten dreizehn regulären Polyeder, doch sind seine
Schriften hierzu verloren gegangen. Die Archimedischen Körper sind
von Johann Kepler (1571-1630) erneut untersucht
worden. Ihm gelang erstmals ihre Aufzählung, das heißt die
Aufstellung einer vollständigen Liste und der Nachweis der Vollständigkeit
der Liste. Die Methode von Kepler erfordert drei Schritte.
1. Im ersten Schritt wird eine Liste aufgestellt, welche
regelmäßigen Polygone zu einer Ecke mit einer
Winkelsumme < 360° kombiniert werden können.
2. Im zweiten Schritt ist zu prüfen, ob mit jeweils einer Art dieser
Ecken ein geschlossenes Polyeder konstruiert werden kann. Dies erweist sich
als nicht immer möglich.
3. Schließlich muss gezeigt werden, dass die zweite Bedingung der
Definition erfüllt ist.
Es liegt dann entweder ein semireguläres Prisma oder Antiprisma vor
oder andernfalls ein Archimedischer Körper.
Wir behandeln hier nur wenige Beispiele. Einige der Archimedischen Körper
können aus Platonischen Körpern durch Abschneiden oder Kappen der
Ecken erhalten werden. Wir zeigen dies an einem Würfel
. Wir schneiden alle acht Ecken so
ab, dass die Schnittebene senkrecht zur jeweiligen Raumdiagonalen steht. Das
Ergebnis hängt davon ab, wie weit die Schnittebene von der Ecke weg in
Richtung auf das Zentrum gelegt wird.
– Den ersten Archimedischen Körper (Abb. links) erhält man, wenn von
den Quadraten des Würfels regelmäßige Achtecke übrig
bleiben. Das ist der abgestumpfte Würfel aus
acht gleichseitigen Dreiecken und sechs regelmäßigen Achtecken.
– Wenn die Würfelkanten gerade verschwinden, erhält man als zweiten
Archimedischen Körper das Kuboktaeder (Abb.
Mitte) aus acht gleichseitigen Dreiecken und sechs Quadraten. Dieses Polyeder
tritt häufig in kubischen Festkörperstrukturen auf.
– Wenn man noch tiefer schneidet, treten statt der Dreiecke Sechsecke auf.
Der nächste Archimedische Körper (Abb. rechts) ist das abgestumpfte Oktaeder aus sechs Quadraten und acht
regelmäßigen Sechsecken. Man kann die Entstehung dieses
Körpers leichter nachvollziehen, wenn man vom Oktaeder ausgeht und
dessen Ecken kappt.
– Wenn schließlich von den Quadraten nur noch die Mittelpunkte
übrig bleiben, ist der resultierende Körper ein reguläres Oktaeder.

Wir halten nochmals fest, was wir hier lernen.
1. Die Symmetrie aller Polyeder, die wir beim Kappen durchlaufen, ist immer die
gleiche: die oktaedrische Symmetrie Oh, unabhängig davon,
wie tief die Schnittebene gelegt wird!
2. Wenn senkrecht zu einer C3-Achse Sechsecke auftreten,
müssen diese nicht regelmäßig sein. Das Gleiche gilt für
die Achtecke senkrecht zu einer C4-Achse. Die angeführten
Archimedischen Polyeder erscheinen als spezielle Fälle, bei denen die
Sechs- bzw. Achtecke gerade regelmäßig sind.
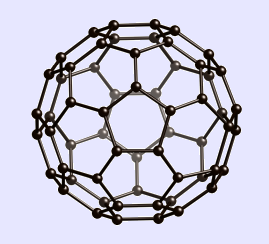
Es gibt ein weiteres Beispiel, das man nicht übergehen kann. Wenn man die zwölf Ecken des Ikosaeders ziemlich weit außen kappt, entstehen Polyeder aus 12 regelmäßigen Fünfecken und 20 Sechecken. Wenn die Sechsecke regelmäßig sind, hat man einen weiteren Archimedischen Körper, das abgestumpfte Ikosaeder mit der Symmetrie Ih. Dieses Polyeder liegt der Felderung von Fussbällen zu Grunde. Das Molekül der Kohlenstoff-Modifikation Fulleren C60 hat näherungsweise die Struktur des abgestumpften Ikosaeders mit 12 regelmäßigen Fünfringen und zwanzig Sechsringen; die C-C-Bindungslängen in den Sechsringen sind allerdings nicht exakt gleich.