Zum Inhaltsverzeichnis     Zurück zum Haupttext

Definition und Aufzählung der Platonischen Körper
Die Idee der zueinander dualen Polyeder
Spezielle Ansichten der Platonischen Körper

Die Frage, welche geschlossenen, konvexen Polyeder mit regelmäßigen Vielecken als Begrenzungsflächen konstruiert werden können, hat bereits die antiken griechischen Mathematiker fasziniert. Etwas anders betrachtet ist das auch die Frage, wie man eine Kugelfläche mit regelmäßigen Vielecken annähern kann. Die engste Form des Problems besteht darin, dass nur eine Art von regelmäßigen Vielecken verwendet werden darf. Spätestens seit Plato (427-348/347 v. Chr.) war bekannt, dass es fünf Lösungen gibt. Diese werden als reguläre Polyeder oder als Platonische Körper bezeichnet. Sehr gute Information zu diesem Thema findet man im Internet unter dem Suchwort "Platonische Körper"; siehe insbesondere:

http://www.mathe.tu-freiberg.de/~hebisch/cafe/platonische.html
http://www.did.mat.uni-bayreuth.de/mmlu/platon/lu/Platon.htm

Die Platonischen Körper

Definition
Ein geschlossenes, konvexes Polyeder heißt regulär,
1. wenn es von nur einer Art von konvexen, regelmäßigen Vielecken begrenzt ist und
2. wenn in jeder Ecke gleich viele dieser Polygone zusammentreffen; oder, wenn jede seiner Ecken auf jede andere durch Symmetrieoperationen abgebildet werden kann.

Wir betrachten also ein reguläres Polyeder aus k konvexen, regelmäßgen n-Ecken (n ≥ 3), wobei an jeder Ecke m Polygone oder auch m Kanten zusammentreffen. Die Innenwinkel der n-Ecke betragen 180°(n-2)/n, also 60, 90, 108 und 120° für n = 3, 4, 5 und 6.

Für die Aufzählung der Platonischen Körper folgen wir zunächst Euklid (etwa 300 v. Chr.). Bei einem Körper müssen an jeder Ecke mindestens drei Polygone zusamentreffen (m ≥ 3). Ferner muss an jeder Ecke die Summe aller Innenwinkel < 360° sein. Das ist offenbar nur in folgenden fünf Fällen (in der Abb. von links nach rechts) möglich:

n = 3, m = 3 für die Ecken des regulären Tetraeders
n = 3, m = 4 für die Ecken des regulären Oktaeders
n = 4, m = 3 für die Ecken des Würfels
n = 5, m = 3 für die Ecken des regulären Pentagondodekaeders
n = 3, m = 5 für die Ecken des regulären Ikosaeders

Ausgehend vom Eulerschen Polyedersatz kann man zum gleichen Ergebnis kommen. Es gilt:
für die Zahl der Ecken E = kn/m,
für die Zahl der Flächen F = k und
für die Zahl der Kanten K = kn/2.
Einsetzen in den allgemeinen Ausdruck für den Eulerschen Polyedersatz ergibt
kn/m + k - kn/2 = 2
und nach Division durch kn
1/m + 1/n - 1/2 = 2/kn
Aus der zweiten Form der Gleichung ersieht man leicht, dass die oben schon genannten fünf Zahlenpaare m ≥ 3 und n ≥ 3 positive Werte für die linke Seite der Gleichung ergeben und damit mögliche Lösungen sind. [Werte n < 3 sind vom Ansatz her ausgeschlossen und formal mögliche Werte m < 3 entsprechen nicht einem räumlichen Gebilde.]

Aus der Anschauung wissen wir, dass die gefundenen fünf Lösungen tatsächlich den fünf Platonischen Körpern entsprechen. Wir wollen nicht übersehen, dass die beiden Ableitungen nichts darüber sagen, ob die fünf Polyeder konstruierbar sind. Das ist ein eigenes Problem.

Die Idee der zueinander dualen Polyeder

Wir erklären dieses von Johann Kepler (1571-1630) eingeführte Konzept am Beispiel des Würfels.

Wenn man die Flächenmitten des Würfels durch Geraden verbindet, wird dem Würfel ein reguläres Oktaeder einbeschrieben. Bei dieser Konstruktion tritt an die Stelle jeder Fläche eine Ecke und an die Stelle jeder Ecke eine Fläche; die Zahl der Kanten bleibt ungeändert. Man bemerkt folgende Punkte:
1. Der Eulersche Polyedersatz bleibt gültig. Es werden lediglich die Summanden Eckenzahl und Flächenzahl vertauscht.
2. Die Symmetrie ändert sich nicht. Ein reguläres Oktaeder hat die gleiche Symmetrie O_h wie der Würfel.
3. Wenn man die gleiche Konstruktion auf ein Oktaeder anwendet, erhält man wieder einen Würfel. Man sagt: Würfel und Oktaeder sind zueinander duale Polyeder.

Wenn man die Idee der dualen Polyeder auf die anderen Platonischen Körper anwendet, zeigt sich:
1. Das reguläre Ikosaeder und das reguläre Pentagondodekaeder sind zueinander dual.
2. Das reguläre Tetraeder ist zu sich selbst dual.

Spezielle Ansichten der Platonischen Körper

In Darstellungen von regulären Polyedern sieht man in der Regel nur die Hälfte der Flächen. Interessante und manchmal überraschende Einblicke in die Symmetrie des Polyeders erhält man, wenn man längs der Drehachsen des Polyeders blickt. Man findet einige dieser Projektionen in den folgenden Abbildungen.

Wir betrachten einen Würfel längs einer der C₂-Achsen, die durch Paare von Kantenmitten gehen (Abb. links). Ferner schauen wir längs einer Raumdiagonalen oder C₃-Achse des Würfels (Abb. rechts). In der zweiten Perspektive ergibt die Parallelprojektion ein regelmäßiges Sechseck als Umriss.

Beim regulären Oktaeder schauen wir längs einer C₂-Achse (Abb. links), längs einer C₃-Achse (Abb. Mitte) und längs einer C₄-Achse (Abb. rechts). Beim Blick längs der C₃-Achse ergibt sich wieder ein regelmäßiges Sechseck als Umriss.

Beim regulären Tetraeder demonstriert der Blick längs einer C₂-Achse (Abb. links), dass die C₂-Achse Teil einer S₄-Achse ist. Eine Beziehung zur trigonalen Pyramide ist aus der Projektion längs einer C₃-Achse zu ersehen (Abb. rechts).

Das reguläre Ikosaeder besitzt C₂-Achsen (dazu Abb. links), C₃-Achsen (dazu Abb. Mitte) und C₅-Achsen (dazu Abb. rechts). Besonders die linke Ansicht ist nicht leicht zu begreifen. Wem die folgende Erläuterung zu schwierig ist, könnte der Bau eines Modells helfen. In der linken Abbildung erscheinen zwei Kanten auf halber Höhe rechts und links als Punkte; das ergibt sich so bei der verwendeten Parallelprojektion. Man kann drei zueinander orthogonale Ebenen erkennen, eine definiert durch die zwei waagerechten Kanten oben und unten, eine definiert durch die zu Punkten reduzierten Kanten rechts und links und eine definiert durch die in der Mitte stehende Kante und ihr nicht sichtbares Gegenstück auf der Rückseite. Die drei Ebenen entsprechen einer D_2h-Symmetrie. Anders ausgedrückt: Sie zeigen, dass die Gruppe D_2h eine Untergruppe der Ikosaedergruppe I_h ist. Aber mehr noch! Die drei Ebenen bilden einen Propeller, dessen Achse eine der C₃-Achsen des Ikosaeders ist. Also ist auch die Gruppe T_h eine Untergruppe der Ikosaedergruppe I_h.

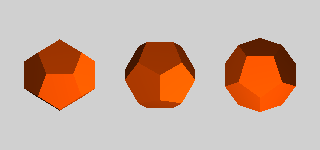
Das reguläre Pentagondodekaeder besitzt C₂-Achsen (dazu Abb. links), C₃-Achsen (dazu Abb. Mitte) und C₅-Achsen (dazu Abb. rechts). Auch hier ist die linke Ansicht nicht leicht zu verstehen. Sie zeigt die gleichen Besonderheiten, die wir schon beim regulären Ikosaeder beschrieben haben.

  Übungen

  smx-projekt@ac.rwth-aachen.de