Zum Inhaltsverzeichnis     Zurück zum Haupttext

n-seitige Pyramiden (n ≥ 3) sind die charakteristischen Körper der Punktgruppen C_nv. Sie bauen sich über n-zähligen Polygonen auf und besitzen n vertikale Spiegelebenen. In der Abb. ist bei der trigonalen Pyramide eine Spiegelebene gezeigt; bei der tetragonalen Pyramide sind es zwei.

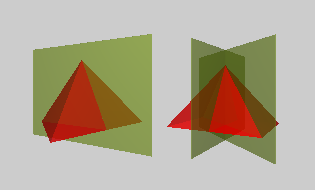
Die Seitenflächen sind gleichschenkelige Dreiecke. Für die folgende Feststellung wollen wir von den Schenkellinien und der Mittellinie einer Seitenfläche sprechen.
– Für ungerade n (n = u) gehen die Spiegelebenen jeweils durch eine Schenkellinie und eine Mittellinie. Alle Spiegelebenen sind von gleicher Art. Wir haben n Spiegelebenen σ_v.
– Für gerade n (n = g) gibt es zwei Arten von Spiegelebenen. Die eine Hälfte davon geht durch zwei gegenüber liegende Schenkellinien, die andere durch zwei gegenüber liegende Mittellinien. Wir haben n/2 Spiegelebenen σ_v und n/2 Spiegelebenen σ_d. [Nebenbemerkung: Bei der quadratischen Grundfläche der tetragonalen Pyramide enthält die zweite Art von Spiegelebenen eine Diagonale der quadratischen Grundfläche; darauf spielt das Subskript d an.]

  smx-projekt@ac.rwth-aachen.de