Zum Inhaltsverzeichnis
Zurück zum Haupttext
Zum Inhaltsverzeichnis
Zurück zum Haupttext
Worum geht es hier?
Netze im zweidimensionalen Raum
Polyeder im dreidimensionalen Raum
Der Eulersche Polyedersatz ist ein Fundamentalsatz der Topologie, gehört also zur Mathematik. Im Kontext der Symmetrielehre dient er uns als wichtiges Hilfsmittel.
Satz:
Für einfache, geschlossene Polyeder mit E Ecken,
F Flächen und K Kanten gilt der Satz:
E - K + F = 2
Der Eulersche Polyedersatz war vermutlich bereits Archimedes (287-212 v. Chr.) bekannt. Er wurde 1640
von René Descartes (1596-1650) und 1752
nochmals von Leonhard Euler (1707-1783) wieder
entdeckt. Wir verifizieren den Satz, z.B. für ein trigonales Prisma.
Hier ist E = 6, K = 9 und F = 5. Es gilt also:
6 - 9 + 5 = 2
so wie es der Eulersche Polyedersatz verlangt.
Wenn wir ein neues Polyeder betrachten und seine Symmetrieelemente suchen wollen, ist es sehr hilfreich, zuerst die Zahl seiner Ecken, Kanten und Flächen abzuzählen. Um das Ergebnis zu kontrollieren, muss man den Eulerschen Polyedersatz verifizieren. Danach wird man die Symmetrieelemente viel leichter in der richtigen Anzahl auffinden können. Das gilt besonders bei großen, hochsymmetrischen Polyedern.
Als Beispiel betrachten wir einen Würfel. Hier ist E = 8, K = 12 und F = 6; der Eulersche Polyedersatz (8 - 12 + 6 = 2) ist erfüllt. Die C3-Achsen enthalten jeweils eine Raumdiagonale und gehen durch zwei Ecken. Da der Würfel acht Ecken besitzt, muss es vier C3-Achsen geben. Die C4-Achsen gehen durch Paare der quadratischen Seitenflächen und sind dreifach vorhanden. Beim Blick auf eine Kante finden wir eine C2-Achse, die durch ein Paar gegenüber liegender Kantenmitten geht. Da es zwölf Kanten gibt, muss es insgesamt sechs solche C2-Achsen geben. Die Drehspiegelachsen können wir in gleicher Weise suchen und sicher abzählen ...
Wer sich für den Beweis des Eulerschen Polyedersatzes nicht interessiert, sollte den Rest dieses Kapitels überspringen.
Wir betrachten nochmals einen Würfel. Seine Ecken und Kanten bilden zusammen ein Netz im dreidimensionalen Raum. Wenn wir erlauben, dass sich die Längen einzelner Kanten frei ändern, können wir dieses Netz vom Würfel herunterziehen und in eine Ebene legen. Das erhaltene Diagramm heißt Schlegeldiagramm des Würfels.
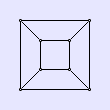
Die Kugel gibt uns das Urbild eines geschlossenen Körpers mit einer einfach zusammenhängenden Oberfläche. Einfache, geschlossene Polyeder haben wie die Kugel eine einfach zusammenhängende Oberfläche. Bei diesen Polyedern kann man, wie wir es für den Wüfel beschrieben haben, Schlegeldiagramme konstruieren.
Um den Eulerschen Polyedersatz zu beweisen, machen wir im Folgenden zwei Schritte. Zuerst sehen wir uns Netze in der Ebene an. Dann bringen wir die Netze zurück in den dreidimensionalen Raum und erzeugen daraus wieder die entsprechenden Polyeder.
Ein Netz besteht aus Knoten und Kanten. Die Knoten entsprechen den Ecken von Polygonen
oder im dreidimensionalen Raum von Polyedern; und die Kanten sind die Strecken, die je zwei
Knoten verbinden. Wir betrachten nun zwei minimale Netze:
1. eine Strecke mit zwei Knoten. Hier ist E = 2 und K = 1.
Die Anzahl der Flächen ist Null, F = 0.
2. ein Dreieck. Hier ist E = 3, K = 3 und F = 1.
Offenbar gilt in beiden Fällen:
E - K + F = 1.
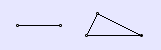
Wir können unser Ergebnis verallgemeinern, indem wir die Netze
systematisch vergrößern. Dafür gibt es genau zwei Möglichkeiten:
1. Anbau an einen Knoten, d.h. Anfügen einer Kante mit
einem neuen Knoten (zwei Beispiele, links; die
angefügte Kante ist rot und gelb markiert). Dabei ist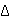 
E =
1, 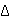K = 1 und 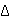F = 0. Die Beziehung
E - K + F = 1
bleibt gültig.
2. Verknüpfung zweier Knoten, d.h. Einfügen einer Kante
zwischen zwei Knoten (drei Beispiele, rechts; die eingefügte Kante
ist gelb und rot markiert). Dabei ist 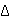E = 0, 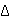K = 1 und 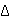F = 1; es kommt eine neue Fläche dazu. Die Beziehung
E - K + F = 1
bleibt ebenfalls gültig.
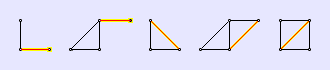
Fazit: Wir können beliebige Netze aus einem minimalen Netz schrittweise aufbauen. Der Eulersche Satz in seiner Version für den zweidimensionalen Raum ist für alle diese Netze gültig.
Im zweiten Schritt bringen wir die Netze in den dreidimensionalen Raum. Wir trachten dabei nur Netze, in deren Knoten mindestens drei Kanten zusammen laufen. Wir wissen ja schon, dass in den Ecken von Polyedern mindestens drei Kanten zusammen treffen müssen. Das kleinst mögliche Netz muss wenigstens vier Knoten haben, weil wir mit drei Knoten nur eine Ebene, nicht ein dreidimensionales Objekt errichten können.
Als Beispiel verwenden das Schlegeldiagramm eines Tetraeders (Abb. links).
Es hat vier Knoten, in denen jeweils drei Kanten zusammen laufen. Wir gehen
nun in den dreidimensionalen Raum und ziehen einen der vier Knoten aus der
Ebene heraus. Das Ergebnis ist ein offenes Tetraeder; im Bild kann man die
blau dargestellten Innenseiten des Tetraeders sehen. Zuletzt schließen
wir das Tetraeder, indem wir ein Dreieck hinzufügen; bei dieser
Operation ist 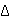F = 1, während die Anzahl der Ecken und Kanten
unverändert bleibt. Damit ist für unser Beispiel der Eulersche
Polyedersatz bewiesen.
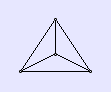
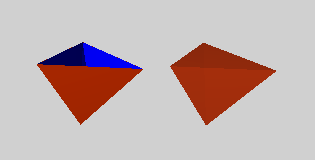
Mit vielen größeren Netzen kann man genauso verfahren. Man wählt, wenn möglich, einen geschlossenen Zug von Kanten, so dass das Netz völlig innerhalb des Kantenzugs zu liegen kommt. Dann zieht man diesen Kantenzug nach einer Seite aus der Ebene heraus und erhält ein offenes Polyeder. Man muss dann noch ein Polygon, welches zu dem Kantenzug passt, hinzufügen, um das Polyeder zu schließen. In all diesen Fällen ist der Eulersche Polyedersatz erfüllt.
Schlussbemerkung:
Unsere Überlegungen haben sich ganz auf die Anschauung gestützt. Die
Frage, welche zusätzlichen Bedingungen notwendig
sind, damit das beschriebene Vorgehen überhaupt möglich ist, haben
wir nicht diskutiert. Mehr zur Bedeutung des
Eulerschen Polyedersatzes in der Topologie und zu seinem Beweis findet man
in der mathematischen Fachliteratur oder im Internet unter dem Suchwort
"Eulerscher Polyedersatz"; siehe z.B.:
http://btmdx1.mat.uni-bayreuth.de/~rockstroh/m_ekf.htm
http://de.wikipedia.org/wiki/Eulerscher_Polyedersatz
