 2.7.1. Allgemeine Aspekte
2.7.1. Allgemeine Aspekte
 2.7.2. Punktgruppen mit höchstens einer Dreh- oder Drehspiegelachse
2.7.2. Punktgruppen mit höchstens einer Dreh- oder Drehspiegelachse
 2.7.3. Diedergruppen
2.7.3. Diedergruppen
 2.7.4. Hochsymmetrische Punktgruppen
2.7.4. Hochsymmetrische Punktgruppen
 2.7.5. Eine provisorische Schlussbemerkung
2.7.5. Eine provisorische Schlussbemerkung
In diesem Kapitel befassen wir uns nochmals mit der systematischen Aufzählung der Punktgruppen, jetzt aus der Sicht des Hermann-Mauguin-Systems.
Die Übersetzung der Symbole vom einen in das andere System ist mühsam. Wir
raten alle Aussagen, die nicht unmittelbar einleuchten, mit Hilfe von
Stereogrammen nachzuvollziehen. Die
Stereogramme der Punktsymmetrien beschreiben die Symmetrie ja unabhängig
davon, ob man gerade das Schoenflies- oder das Hermann-Mauguin-System
benutzt.
Wir erinnern uns: Es gibt unendlich viele Punktgruppen; die Zähligkeit von Drehachsen und Drehspiegelachsen bzw. Inversionsachsen ist nicht begrenzt. Autoreifen und Zahnräder sind bekanntlich Beispiele für Alltagsobjekte, deren Punktgruppen Drehachsen hoher Zähligkeit aufweisen.
Bei klassischen Kristallen, also dreidimensional-periodischen Festkörpern, ist das nicht so. Wir nehmen ohne Beweis zur Kenntnis, dass nur 2-, 3-, 4- und 6-zählige Drehachsen und Inversionsachsen mit der Symmetrie klassischer Kristalle vereinbar sind. Wir haben es nicht mehr mit unendlich vielen, sondern nur mit einer definierten und kleinen Zahl, nämlich mit 32 Punktgruppen zu tun. Diese 32 Punktgruppen heißen kristallographische Punktgruppen. Man hat schon im 18. Jahrhundert begonnen, Kristalle nach ihrer Symmetrie zu klassifizieren, und hat dabei 32 Kristallklassen gefunden. Die beiden Begriffe "kristallographische Punktgruppen" und "Kristallklassen" werden heute oft wie Synonyme gebraucht.
Das Hermann-Mauguin-System wird üblicherweise von Kristallographen, Festkörperchemikern und Festkörperphysikern benutzt. Deshalb sind Punktgruppensymbole nach Hermann-Mauguin nur für die 32 kristallographischen Punktgruppen gebräuchlich, obwohl auch dieses System prinzipiell auf alle Punktgruppen anwendbar ist.
In Kapitel 2.6 hatten wir gelernt, dass unterschiedliche Spiegelebenen im Hermann-Mauguin-System nicht wie bei Schoenflies durch verschiedene Symbole unterschieden werden, sondern durch ihre Anordnung im Punktgruppensymbol. Die Reihenfolge der Symmetrielemente im Hermann-Mauguin-Symbol wird bei den kristallographischen Punktgruppen mit Hilfe der Vorzugsrichtungen der Kristalle, den so genannten Blickrichtungen, festgelegt. In den meisten Lehrbüchern findet man deshalb zuerst Erläuterungen zum Kristallbau und dann darauf aufbauend die Aufzählung der Punktgruppen; dabei beschränkt man sich natürlich auf die 32 kristallographischen Punktgruppen. Dagegen wollen wir in diesem Kapitel eine systematische Aufzählung aller Punktgruppen nach Hermann und Mauguin präsentieren.
Wir beginnen die Aufzählung mit den Punktgruppen, die durch eine Drehachse (und nichts mehr) erzeugt werden (1. Klasse). Es folgen die Punktgruppen, die durch eine Inversionsachse (und nichts mehr) erzeugt werden (2. Klasse). Danach nehmen wir vertikale Spiegelebenen (3. Klasse) bzw. horizontale Spiegelebenen (4. Klasse) hinzu.
1. Punktgruppen mit einer Drehachse
Bei diesen einfachsten Gruppen ist die Entsprechung zum Schoenflies-System trivial.
HM: 1, 2, 3, ...
SS: Cn =
[Cn] mit n = 1, 2, 3, ...
2. Punktgruppen mit einer Inversionsachse
HM:
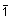 ,
,
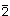 = m,
= m,
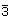 ,
,
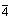 , ...
, ...
Bezüglich der Entsprechung zum Schoenflies-System muss man drei Unterklassen unterscheiden.
1. HM: 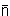 =
= 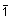 ,
,
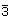 ,
,
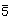 , ... mit ungeradem
n.
, ... mit ungeradem
n.
SS: Cni =
[Cn, i] mit n = 1, 3, 5, ...
2. HM: 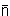 =
= 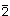 ,
,
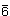 ,
,
 , ... mit doppelt
ungeradem n.
, ... mit doppelt
ungeradem n.
SS: C(n/2)h =
[C(n/2), σh] mit n/2 = 1, 3, 5, ...
3. HM: 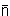 =
= 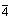 ,
,
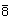 , ... mit doppelt
geradem n.
, ... mit doppelt
geradem n.
SS: Sn =
[Sn] mit n = 4, 8, ...
3. Punktgruppen mit einer Drehachse und vertikalen Spiegelebenen
Im Hermann-Mauguin-System wird zwischen den Gruppen mit geradem n und denen mit ungeradem n unterschieden.
HM, n = g: 2mm, 4mm, 6mm, ...
HM, n = u: 3m, 5m, ...
SS: Cnv =
[Cn, σv] mit n = 2, 3, ∞
Für ungerades n gibt es nur eine Art von vertikalen
Spiegelebenen; die Gruppensymbole 3m, 5m usw. zeigen neben der Drehachse
nur ein "m". Dagegen gibt es für gerades n zwei Arten
von Spiegelebenen; die Gruppensymbole 2mm, 4mm, 6mm usw. haben deshalb zwei
"m". Dieser Unterschied kommt in den Stereogrammen der Gruppen 2mm
(C2v) und 3m (C3v) sehr deutlich zum
Ausdruck.
Entsprechend dem minimalistischen Stil des Hermann-Mauguin-Systems
findet man in älteren Texten für die Gruppe 2mm die kürzere
Schreibung mm, weil die zweizählige Achse durch die zwei Spiegelebenen
bereits impliziert ist; später ist 2mm konventionell geworden, um
die Ähnlichkeit zu den anderen Gruppen 4mm, 6mm usw. zu wahren.
4. Punktgruppen mit einer Drehachse und einer horizontalen Spiegelebene
Hier muss man wieder zwischen den Gruppen mit geradem n und denen mit ungeradem n unterscheiden.
1. HM, n = g: 2/m, 4/m, 6/m, ...
SS: Cnh = [Cn,
σh] mit n = 2, 4, 6, ...
Diese Gruppen sind neu.
2. HM, n = u:
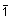 ,
,
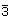 ,
,
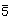 , ...
, ...
SS: Cni =
[Cn, i] mit n = 1, 3, 5, ...
Diese Gruppen sind bereits unter 2. aufgetreten.
Die Gruppensymbole n/m werden "n über m" gesprochen. Man schreibt sie oft wie einen Bruch mit waagerechtem Strich für die Spiegelebene, um an die horizontale Stellung zur Drehachse zu erinnern.
Wir fassen die Ergebnisse dieses Unterkapitels in einer Tabelle zusammen, die eine Übersicht über die Gruppensymbole im Hermann-Mauguin- und im Schoenflies-System gibt.
 Tabelle: Schoenflies- und Hermann-Mauguin-Notation für diese
Gruppen
Tabelle: Schoenflies- und Hermann-Mauguin-Notation für diese
Gruppen
Wir erzeugen jetzt die Diedergruppen, indem wir zu den Gruppen der obigen Klassen 1. - 4. zweizählige Nebenachsen hinzufügen.
5. Diedergruppen: Gruppen mit einer n-zähligen Hauptachse und
zweizähligen Nebenachsen
Wir unterscheiden zwischen den Gruppen mit geradem n und denen mit ungeradem n. Die Situation ist ganz ähnlich wie oben in der 3. Klasse.
HM, n = g: 222, 422, 622, ...
HM, n = u: 32, 52, ...
SS: Dn =
[Cn, C2] mit n = 2, 3,
...
Für ungerades n gibt es nur eine Art von Nebenachsen; die
Gruppensymbole 32, 52 usw. zeigen neben der Hauptachse nur eine "2"
für die Nebenachsen. Dagegen gibt es für gerades n zwei Arten
von Nebenachsen; die Gruppensymbole 222, 422, 622 usw. enthalten deshalb
zweimal eine "2". Dieser Unterschied ist in den Stereogrammen
der Gruppen 222 (D2) und 32 (D3) sehr
schön zu sehen.
6. Diedergruppen mit einer n-zähligen Inversionsachse und
zweizähligen Nebenachsen
Da wir drei Arten von Inversionsachsen haben, müssen drei Unterklassen untersucht werden.
1. HM: 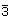 m,
m, 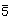 m, ... mit
ungeradem n.
m, ... mit
ungeradem n.
SS: Dnd =
[Cn, C2, σv] mit
n = 3, 5, ...
Beispielsweise entspricht das
Hermann-Mauguin-Symbol 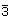 m
dem Schoenflies-Symbol D3d.
m
dem Schoenflies-Symbol D3d.
2. HM:
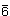 2m,
2m,
 2m, ... mit doppelt
ungeradem n.
2m, ... mit doppelt
ungeradem n.
SS: D(n/2)h =
[C(n/2), C2, σh] mit
n/2 = 3, 5, ...
Es entspricht also z.B. das Symbol
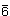 m2 dem Schoenflies-Symbol D3h.
m2 dem Schoenflies-Symbol D3h.
3. HM: 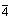 2m,
2m,
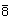 2m, ... mit doppelt
geradem n.
2m, ... mit doppelt
geradem n.
SS: D(n/2)d =
[C(n/2), C2, σd] mit
n = 4, 8, ...
Hier entspricht
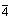 2m dem
Schoenflies-Symbol D2d.
2m dem
Schoenflies-Symbol D2d.
Anmerkungen
1. Die Inversionsachsen 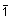 und
und 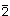 können bei den Diedergruppen nicht vorkommen.
können bei den Diedergruppen nicht vorkommen.
2. Die angegebenen Entsprechungen sollte man wieder durch Konstruktion der
Stereogramme verifizieren.
3. Das Beipiel 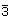 m haben wir
erhalten, indem wir zu
m haben wir
erhalten, indem wir zu 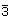 eine zweizählige Nebenachse hinzugefügt haben. Dabei entstehen
diagonale Spiegel. Das Hermann-Mauguin-System gibt Spiegeln den höheren
Rang; deshalb im Symbol der Spiegel statt der zweizähligen
Nebenachse.
eine zweizählige Nebenachse hinzugefügt haben. Dabei entstehen
diagonale Spiegel. Das Hermann-Mauguin-System gibt Spiegeln den höheren
Rang; deshalb im Symbol der Spiegel statt der zweizähligen
Nebenachse.
4. Bei den Symbolen 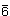 2m und
2m und
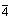 2m gibt es noch formale
Details, die wir mit den einfachen bisherigen Mitteln nicht begründen
können. Das muss der Sauberkeit halber angemerkt werden; wir raten
aber, sich hier nicht aufzuhalten
2m gibt es noch formale
Details, die wir mit den einfachen bisherigen Mitteln nicht begründen
können. Das muss der Sauberkeit halber angemerkt werden; wir raten
aber, sich hier nicht aufzuhalten
7. Die noch fehlenden Diedergruppen mit einer horizontalen Spiegelebene
Wir fahren mit unserer Aufzählung fort, indem wir zu den Gruppen der obigen dritten Klasse zweizählige Nebenachsen hinzufügen. Da schon vertikale Spiegel vorliegen, entsteht mit dem Hinzufügen der Nebenachsen eine horizontale Spiegelebene.
1. HM (aus 2mm, 4mm, ...): mmm, 4/mmm, 6/mmm, ...
SS: Dnh =
[Cn, C2, σh] mit
n = 2, 4, 6, ...
Diese Gruppen sind die bisher noch fehlenden
Diedergruppen.
2. HM (aus 3m, 5m, ...):
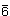 m2,
m2,
 m2, ...
m2, ...
SS: Dnh =
[Cn, C2, σh] mit
n = 3, 5, ...
Diese Diedergruppen sind bereits in der 6. Klasse (Unterklasse 2) enthalten.
In der ersten Unterklasse zeigt das Gruppensymbol die Zähligkeit der
Hauptachse, die hinzugekommene horizontale Spiegelebene und die zwei Arten
vertikaler Spiegelebenen an. Wenn alle drei Achsen zweizählig sind, hat
man ein Tripel aufeinander senkrecht stehender Spiegelebenen. Das Gruppensymbol
ist hier mmm (statt 2/mmm). Die Anwesenheit der zweizähligen Achsen ist
implizit.
Anmerkung
Es verbleibt oben noch die 4. Klasse, zu der wir zweizählige
Nebenachsen hinzufügen können. Wir erwarten natürlich nicht,
noch neue Diedergruppen zu finden, und verzichten deshalb auf die tatsächliche
Durchführung.
Wir fassen auch dieses Unterkapiel in einer Tabelle zusammen, die eine Übersicht über die Gruppensymbole im Hermann-Mauguin- und im Schoenflies-System gibt.
 Tabelle: Schoenflies- und Hermann-Mauguin-Notation für diese
Gruppen
Tabelle: Schoenflies- und Hermann-Mauguin-Notation für diese
Gruppen
Die hochsymmetrischen Punktgruppen besitzen mehrere Achsen mit Zähligkeiten n > 2. Es gibt bekanntlich 7 hochsymmetrische Punktgruppen, die wir mit ihren Hermann-Mauguin-Symbolen hier auflisten.
1. 23 für die tetraedrische
Drehgruppe (T)
2. 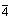 3m (Td)
3m (Td)
3. m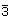 (Th)
(Th)
4. 432 für die oktaedrische
Drehgruppe (O)
5. m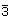 m (Oh)
m (Oh)
6. 532 für die ikosaedrische
Drehgruppe (I)
7. 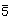
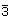 m
(Ih)
m
(Ih)
Anmerkungen
1. Die Punktgruppen 1 - 5 sind die kubischen Punktgruppen. Die erste
Blickrichtung ist durch das orthogonale Achsendreibein gegeben. Die zweite
ist die Richtung der dreizähligen Achse, die dritte ist die Richtung
der zweizähligen Achse von Kubus und Oktaeder. Dies ergibt die Symbole
der Gruppen 23 und 432.
2. Wenn Spiegelsymmetrie hinzukommt, werden statt der Drehachsen die
Inversionsachsen in den gleichen Blickrichtungen genannt. Wenn zu einer Achse
eine horizontale Spiegelebene vorliegt, wird statt der Achse der Spiegel im
Symbol genannt. So steht im Symbol m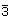 m das erste m für die zu den vierzähligen Achsen
horizontalen Spiegelebenen und das zweite für die zu den
zweizähligen Achsen horizontalen Spiegelebenen.
m das erste m für die zu den vierzähligen Achsen
horizontalen Spiegelebenen und das zweite für die zu den
zweizähligen Achsen horizontalen Spiegelebenen.
3. Die fünfzähligen Drehachsen der Ikosaedergruppe sind nicht
kompatibel mit einem dreidimensional-periodischen Kristallbau. Es kann im
klassischen Kristall keine fünfzählige Symmetrie geben.
Moleküle mit ikosaedrischer Symmetrie werden im Kristall durch
Gitterkräfte unter Symmetrieernierdrigung deformiert.
4. Die Kristallographie kann deshalb für den Fall ikosaedrischer
Symmetrie keine Blickrichtungen angeben. Das Symbol 532 nennt
die drei Arten von Drehachsen nach abnehmender Zähligkeit. Wenn
Spiegelsymmetrie hinzukommt, treten an die Stelle der Drehachsen wieder
Inversionsachsen. Das ergibt das Symbol
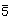
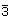 m.
m.
Das ganze zweite Kapitel des SMX-Projekts war den Punktsymmetrien gewidmet. Zuletzt mussten wir in unseren Erklärungen auf die Kristallographie verweisen, also den bisher selbst gesteckten Rahmen überschreiten. Wenn das SMX-Projekt Leser, freundliche Kritiker und Mitmacher findet, sollten weitere Kapitel die Ideen des Kapitels 1.2 wieder aufgreifen und uns über die translatorische Symmetrie zu den Schönheiten des Kristallbaus führen.
Wir fügen zwei Bilder an, die diesen Gedanken stärken sollen: eines von einem Kupfer(II)-sulfat-pentahydrat-Kristall aus dem Grundpraktikum und eines von einem nicht näher definierten Kristall aus dem Schlenkrohr eines Doktoranden. Hätten wir nicht den Grund und die intellektuelle Neugierde, hier weiter zu studieren?

