Zum Inhaltsverzeichnis     Zurück zum Haupttext

In der folgenden Tabelle geben wir einen Überblick über die Punktgruppen in Hermann-Mauguin-Notation und in Schoenflies-Notation. Die Spalten geben an:
 HM: Hermann-Mauguin-Symbol
 SS: Schoenflies-Symbol
 XX: Ob die Punktgruppe bei Kristallen und bei Molekülen in Kristallen möglich ist
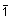 : Ob Zentrosymmetrie vorliegt
 m: Wieviele Spiegelebenen vorliegen
 Drehachse: Art der Achse
 Inversionsachse: Art der Achse

HM	SS	XX		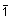m	Drehachsen	Inversionsachsen
1	C1	+	-	-	-	-
2	C2	+	-	-	2	-
3	C3	+	-	-	3	-
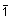	Ci	+	+	-	-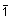
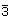	C3i	+	+	-	3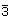
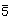	C5i	-	+	-	5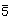
m (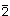)	Cs	+	-	1x	-	-
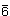	C3h	+	-	1x	3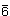
	C5h	-	-	1x	5
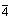	S4	+	-	-	2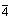
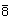	S8	-	-	-	4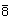
3m	C3v	+	-	3x	3	-
5m	C5v	-	-	5x	5	-
2mm	C2v	+	-	2x	2	-
4mm	C4v	+	-	4x	4	-
6mm	C6v	+	-	6x	6	-
2/m	C2h	+	+	1x	2	-
4/m	C4h	+	+	1x	4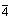
6/m	C6h	+	+	1x	6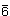

Anmerkungen
1. Punktgruppen können in Kristallen nur vorkommen, wenn die Zähligkeit der Drehachsen und Inversionsachsen n = 1, 2, 3, 4 oder 6 ist. Aber Vorsicht: Für Drehspiegelachsen kann das nicht so einfach formuliert werden.
2. Die Eigenschaft Zentrosymmetrie ist sowohl in der Spektroskopie wie auch in der Kristallographie von großer Bedeutung. Wir erinnern uns z.B. daran, dass chirale Moleküle nicht zentrosymmetrisch sein können.
3. Bei der Gruppen m und 2/m bleibt die letzte Spalte leer, weil 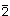bereits bei den Spiegelebenen in Spalte 5 aufgeführt ist.

  smx-projekt@ac.rwth-aachen.de