Stereogramme
Bei der 3. Klasse von Punktgruppen kombinieren wir eine Drehachse mit einer
horizontalen Spiegelebene.
Cnh =
[Cn, σh] mit n = 2, 3, ...
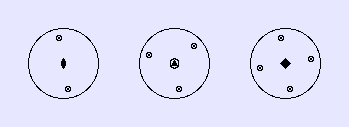
Als Beispiele betrachten wir die Stereogramme der Punktgruppen C2h, C3h und C4h.
Anmerkungen
1. Die Erzeugende zeigt zunächst einmal, dass bei allen Punktgruppen
Cnh eine Drehachse Cn und eine Spiegelebene
σh vorliegen.
2. Die Punktgruppen Cnh mit ungeradem n können
durch eine Drehspiegelung Sn erzeugt werden. Das Stereogramm
ist identisch mit dem der Drehspiegelachse Sn. Das Achsensymbol
stammt wie immer aus dem Hermann-Mauguin-System. Es zeigt die
n-zählige Drehachse mit einer 2n-eckigen Umrahmung. Damit
erinnert es daran, dass die Drehspiegelung Sn von der
Ordnung 2n ist, oder anders ausgedrückt, dass es 2n
äquivalente Punktlagen gibt.
3. Das Stereogramm der Punktgruppen Cnh mit geradem n
zeigt, dass auch ein Symmetriezentrum vorliegt. Dieses wird nicht
angezeigt.
4. Bei geradem n ist in der Cn-Achse eine C2-Achse
enthalten. Die C2-Operation kehrt die Achsenrichtung der
x- und der y-Achse um. Die Spiegelung an σh
kehrt die Achsenrichtung der z-Achse um. Beide zusammen kehren also
alle drei Achsenrichungen um: Das ist eine Inversion i!