Stereogramme
Wir fügen zu den Diedergruppen Dn eine horizontale
Spiegelebene σh hinzu. Die Erzeugende besteht nun
aus drei Symmetrieoperationen.
Dnh = [Cn, C2, σh] mit n = 2, 3, ..., ∞
Die Stereogramme der ersten drei Punktgruppen dieser Klasse D2h, D3h und D4h zeigen die wesentlichen Eigenschaften.
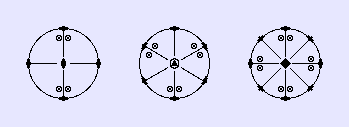
Anmerkungen
1. Wenn man in der Erzeugenden das zweite oder das dritte Element
weglässt, kommt man zu den Untergruppen Dn bzw.
Cnv; der Vergleich mit diesen Punktgruppen ist besonders
lehrreich.
2. Punktgruppen Dnh mit ungeradem n haben
eine Art von Nebenachsen (wie bei den Untergruppen
Dn) und eine Art von vertikalen Spiegelebenen (wie
bei den Untergruppen Cnv). Wegen der Achsensymbole siehe
die Klasse der Gruppen Cnv.
3. Dagegen besitzen die Punktgruppen Dnh
mit geradem n zwei Arten von Nebenachsen, nämlich n/2
Nebenachsen C2' und n/2 Nebenachsen C2". Sie
besitzen auch zwei Arten von Spiegelebenen, nämlich n/2
vertikale Spiegelebenen σv und n/2 diagonale
Spiegelebenen σd. Die Hauptachse enthält
eine C2-Achse. Mit der horizontalen Spiegelebene muss dann auch
ein Symmetriezentrum vorliegen; dieses wird nicht angezeigt.